kryptoanaliza
Kryptoanaliza statystyczna opierających się na fakcie nierównomiernego występowania poszczególnych liter i sylab w językach naturalnych. Jak wyglądałaby prosta kryptoanaliza tego typu szyfru. Tak jak wspominałem na początku, należy zliczyć ilość liter w naszym tekście.
| a | ą | b | c | ć | d | e |
|---|---|---|---|---|---|---|
| 8,91% | 0,99% | 1,47% | 3,96% | 0,40% | 3,25% | 7,66% |
| ę | f | g | h | i | j | k |
| 1,11% | 0,30% | 1,42% | 1,08% | 8,21% | 2,28% | 3,51% |
| l | ł | m | n | ń | o | ó |
| 2,10% | 1,82% | 2,80% | 5,52% | 0,20% | 7,75% | 0,85% |
| p | q | r | s | ś | t | u |
| 3,13% | 0,14% | 4,69% | 4,32% | 0,66% | 3,98% | 2,50% |
| v | w | x | y | z | ź | ż |
Im tekst jest dłuższy, tym nasz szyfr jest łatwiejszy do złamania. Weźmy na ten przykład zaszyfrowaną wiadomość:
Tekst pochodzi ze strony sport.pl i dotyczy rozgrywek piłkarskich naszej reprezentacji.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
Imports System.Windows.Forms Module Module1 Dim wiadomosc As String Dim listZnakow As New List(Of List(Of Char)) Sub Main() Dim open_dialog As New OpenFileDialog() open_dialog.InitialDirectory = "c:\" open_dialog.Filter = "All Files|*.*" If open_dialog.ShowDialog() = System.Windows.Forms.DialogResult.OK Then 'pobiera tekst do zmiennej wiadomosc = IO.File.ReadAllText(open_dialog.FileName) For i As Integer = 0 To wiadomosc.Length - 1 Dim zawiera As Boolean = False For j As Integer = 0 To listZnakow.Count - 1 If listZnakow(j).Contains(wiadomosc(i)) Then listZnakow(j).Add(wiadomosc(i)) zawiera = True Exit For End If Next If zawiera = False Then Dim znak As New List(Of Char) znak.Add(wiadomosc(i)) listZnakow.Add(znak) End If Next listZnakow.Sort(Function(L1 As List(Of Char), L2 As List(Of Char)) (L2.Count).CompareTo(L1.Count)) Dim zlicz As Double = 0 For i As Int32 = 0 To listZnakow.Count - 1 zlicz += listZnakow(i).Count / wiadomosc.Length Console.WriteLine(listZnakow(i)(0) + " stanowi:" + _ (Math.Round(listZnakow(i).Count / wiadomosc.Length, 4) * 100).ToString + " %") Next Console.ReadLine() End If End Sub End Module |
Efekt jest taki, że:
# stanowi:15,61 %
d stanowi:8,88 %
l stanowi:7,71 %
h stanowi:6,54 %
} stanowi:5,95 %
q stanowi:5,27 %
u stanowi:4,39 %
r stanowi:4,39 %
| stanowi:4,1 %
f stanowi:3,8 %
z stanowi:3,51 %
o stanowi:3,22 %
w stanowi:3,02 %
g stanowi:2,63 %
v stanowi:2,54 %
m stanowi:2,15 %
p stanowi:2,05 %
x stanowi:1,85 %
s stanowi:1,76 %
/ stanowi:1,37 %
n stanowi:1,37 %
j stanowi:1,27 %(…)
Z naszej analizy możemy wywnioskować, że „# pozycja ASCII to 35” oznacza literę „a- pozycja ASCII to 97” lub „i-pozycja ASCII to 105″ trzeba pamiętać, że tekst może zawierać puste znaki oddzielające słowa, które też mogą stanowić dużą część tekstu zaszyfrowanego, pozycja pustej przestrzeni ” ” w ASCII to 32, mamy więc:
32-35 = -3
(97-127)-35 = -65
(105-127)-35 = -57
Aby odwrócić szyfrowanie w kodzie podanym powyżej, wystarczy zmienić wartość:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
Imports System.Windows.Forms Module Module1 Dim wiadomosc As String Dim klucz As Integer = -3 Mod 127 Dim wiadomoscZaszyfrowana As String Dim wiadomoscOdszyfrowana As String Sub Main() Dim open_dialog As New OpenFileDialog() open_dialog.InitialDirectory = "c:\" open_dialog.Filter = "All Files|*.*" If open_dialog.ShowDialog() = System.Windows.Forms.DialogResult.OK Then 'pobiera tekst do zmiennej wiadomosc = IO.File.ReadAllText(open_dialog.FileName) For i As Int32 = 0 To wiadomosc.Length - 1 Dim k As Integer = Asc(wiadomosc(i)) If k + klucz < 0 Then wiadomoscZaszyfrowana += Chr(127 + ((k + klucz) Mod 127)) Else wiadomoscZaszyfrowana += Chr((k + klucz) Mod 127) End If Next Console.WriteLine(wiadomoscZaszyfrowana.ToString) Console.ReadLine() End If End Sub End Module |
Pewnie myślicie, że szyfr z kluczem będzie trudniejszy do złamania, nic bardziej mylnego. Wszystko będzie zależało od długości klucza i długości naszej wiadomości. Jeśli odszyfrowaliście tekst powyżej, usuń z niego spacje i zaszyfrujcie go z kluczem „cba” :
Wiadomość jest w miarę długa a klucz krótki. Aby ją złamać, musimy najpierw zgadnąć długość klucza, oczywiście istnieje możliwość, że klucz jest bardzo długi, nawet dłuższy niż sama wiadomość. Nie miałoby to większego sensu, gdyż klucz musi być w jakiś sposób przekazany odbiorcy, nikt nie będzie tworzył szyfru, w którym klucz będzie zbyt długo do przekazania. Będziemy rozkładać klucz litera po literze.
Zakładamy, że nasz klucz jest dwuliterowy, będziemy więc sprawdzać, co drugą literę używając kodu:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 |
Imports System.Windows.Forms Module Module1 Dim wiadomosc As String Dim listZnakow As New List(Of List(Of Char)) Dim dlugoscKlucza As Integer = 2 Dim literaKlucza As Integer = 0 Dim tekst As String Sub Main() Dim open_dialog As New OpenFileDialog() open_dialog.InitialDirectory = "c:\" open_dialog.Filter = "All Files|*.*" If open_dialog.ShowDialog() = System.Windows.Forms.DialogResult.OK Then 'pobiera tekst do zmiennej wiadomosc = IO.File.ReadAllText(open_dialog.FileName) For i As Integer = 0 To wiadomosc.Length - (1 + literaKlucza) If (i Mod dlugoscKlucza) = literaKlucza Then Dim zawiera As Boolean = False tekst += wiadomosc(i) For j As Integer = 0 To listZnakow.Count - 1 If listZnakow(j).Contains(wiadomosc(i)) Then listZnakow(j).Add(wiadomosc(i)) zawiera = True Exit For End If Next If zawiera = False Then Dim znak As New List(Of Char) znak.Add(wiadomosc(i)) listZnakow.Add(znak) End If End If Next Dim wiadomoscZaszyfrowana As String = "" For i As Integer = 0 To wiadomosc.Length - 1 wiadomoscZaszyfrowana += wiadomosc(i) Next Console.WriteLine(wiadomoscZaszyfrowana) Console.WriteLine() Console.WriteLine(tekst) Console.WriteLine() listZnakow.Sort(Function(L1 As List(Of Char), L2 As List(Of Char)) (L2.Count).CompareTo(L1.Count)) For i As Int32 = 0 To listZnakow.Count - 1 Console.WriteLine(listZnakow(i)(0) + " stanowi:" + (Math.Round(listZnakow(i).Count / tekst.Length, 4) * 100).ToString + " % kod ASCII znaku:" + Asc(listZnakow(i)(0)).ToString) Next Console.ReadLine() End If End Sub End Module |
Wiemy, że zaszyfrowany tekst nie ma spacji, wykorzystamy to. sprawdzając co drugą literę:
Weźmiemy pod uwagę trzy litery a- ASCII(97), i- ASCII(105), o- ASCII(111)
G stanowi 6,47% liter teksu, jego numer ASCII to 71
(97-127)-71 =-101 ASCII(101) = e
(105-127)-71 =-93 ASCII(93) = ]
(111-127)-71 =-87 ASCII(87) = W
Pierwszą literą klucza może być e lub ] lub W
Rozważmy drugą literę klucza
Weźmiemy pod uwagę trzy litery a- ASCII(97), i- ASCII(105), o- ASCII(111)
R stanowi 6,48 % liter teksu, jego numer ASCII to 82
(97-127)-82 =-112 ASCII(112) = p
(105-127)-82 =-104 ASCII(104) = h
(111-127)-82 =-98 ASCII(98) = b
Pierwszą literą klucza może być p lub h lub b
Ilość kombinacji, jaką musimy teraz sprawdzić to 3*3 =9, oczywiście żadna z nich nie będzie trafna, a nasz tekst pozostanie zaszyfrowany. Sprawdzamy teraz klucz trzyliterowy:
Weźmiemy pod uwagę trzy litery a- ASCII(97), i- ASCII(105), o- ASCII(111)
M stanowi 9% liter teksu, jego numer ASCII to 77
(97-127)-77 =-107 ASCII(107) = k
(105-127)-77 =-99 ASCII(99) = c
(111-127)-77 =-93 ASCII(83) = ]
Pierwszą literą klucza może być k lub c lub ]
dla drugiej litery klucza, rozkład liter:
Weźmiemy pod uwagę trzy litery a- ASCII(97), i- ASCII(105), o- ASCII(111)
D stanowi 12,85 % liter teksu, jego numer ASCII to 68
(97-127)-68 =-98 ASCII(98) = b
(105-127)-68 =-90 ASCII(90) = Z
(111-127)-68 =-84 ASCII(84) = T
Pierwszą literą klucza może być b lub Z lub T
dla trzeciej litery klucza, rozkład liter:
Weźmiemy pod uwagę trzy litery a- ASCII(97), i- ASCII(105), o- ASCII(111)
C stanowi 10,45 % liter teksu, jego numer ASCII to 67
(97-127)-67 =-97 ASCII(97) = a
(105-127)-67 =-89 ASCII(89) = Y
(111-127)-67 =-83 ASCII(83) = S
Pierwszą literą klucza może być a lub Y lub S
Mamy więc do sprawdzenia: 3*3*3 =27 możliwości
|
|
|
|||
|---|---|---|---|---|---|
| k | b | a | |||
| c | Z | Y | |||
| ] | T | S |
Oczywiście wszystkie te kombinacje powinien wykonywać za nas komputer, szukając konkretnych słów ze słownika. Taki słownik może zawierać łączniki lub słowa, które spodziewamy się znaleźć w wiadomości. Jeśli toczylibyśmy jakąś wojnę, komputer mógłby szukać słowa „atak”, „odwrót” , „wróg”, „pozycja”. Oczywiście model zademonstrowany powyżej jest bardzo wyidealizowany, lecz jego prostota ukazuje możliwości tego sposobu szyfrowania wiadomości i ich łamania. Wraz ze wzrostem długości klucza, rośnie ilość kombinacji, jakie możemy wykonać. Jak więc poznać długość klucza? Można w tym celu wykorzystać test Kasiskiego. Który polega na przeszukiwaniu szyfrogramu w poszukiwaniu powtarzających się sekwencji takich samych znaków. Znalezienie takich sekwencji może oznaczać, że są to takie same fragmenty tekstu jawnego. Zakodowane za pomocą takich samych fragmentów klucza. Im więcej powtórzeń uda się znaleźć w zaszyfrowanym tekście tym większe jest prawdopodobieństwo, że wynikają one z szyfrowania takich samych fragmentów tekstu. Zastosowanie takiej metody prezentuje algorytm poniżej:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 |
Imports System.Windows.Forms Module Module1 Dim wiadomosc As String Dim dlugoscKlucza As Integer = 3 Sub Main() Dim open_dialog As New OpenFileDialog() open_dialog.InitialDirectory = "c:\" open_dialog.Filter = "All Files|*.*" If open_dialog.ShowDialog() = System.Windows.Forms.DialogResult.OK Then 'pobiera tekst do zmiennej wiadomosc = IO.File.ReadAllText(open_dialog.FileName) Dim listaSekwencji As New List(Of List(Of String)) For i As Integer = 0 To wiadomosc.Length - (1 + (wiadomosc.Length Mod dlugoscKlucza)) Step dlugoscKlucza Dim zawiera As Boolean = False Dim sekwencja As String = "" Dim sekwencjaASCII As String = "" For j As Integer = i To i + dlugoscKlucza - 1 sekwencja += wiadomosc(j).ToString + "," Next For j As Integer = 0 To listaSekwencji.Count - 1 If listaSekwencji(j).Contains(sekwencja) Then listaSekwencji(j).Add(sekwencja) zawiera = True Exit For End If Next If zawiera = False Then Dim znak As New List(Of String) znak.Add(sekwencja) listaSekwencji.Add(znak) End If Next listaSekwencji.Sort(Function(L1 As List(Of String), L2 As List(Of String)) (L2.Count).CompareTo(L1.Count)) For i As Int32 = 0 To listaSekwencji.Count - 1 Dim tablica As String() = listaSekwencji(i)(0).Split(",") Console.WriteLine(listaSekwencji(i)(0).ToString + " (" + Asc(tablica(0)).ToString + "," + Asc(tablica(1)).ToString + "," + Asc(tablica(2)).ToString + ") znaleziono sekwencji:" + listaSekwencji(i).Count.ToString) Next Console.ReadLine() End If End Sub End Module |
Powyższy kod prezentuje tekst (bez spacji) zaszyfrowany kluczem „cba” w formie liczbowej ASCII i wyświetla ilość sekwencji:
Pokażę jeszcze jedną metodę prostej kryptoanalizy, jest to metoda słownikowa. Polegająca na siłowym odgadywania kluczy kryptograficznych i haseł do systemów. Polega ona na sukcesywnym testowaniu haseł zawartych w słowniku. Zaszyfrujemy sobie wiadomość z wykorzystaniem autoklucza:
Teraz należy nakreślić algorytm. Jak wiemy ASCII ma tylko 127 znaków, słownik musimy zrobić sobie sami, ale to nie będzie problem, wykorzystamy najczęściej używane słowa w języku polskim lub takie, które mogą znaleźć się w tekście:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 |
Imports System.Windows.Forms Module Module1 Dim wiadomosc As String Dim wiadomoscOdszyfrowana As String Dim listaKluczy As New List(Of Char) Dim slownik() As String = {"ale", "do", "ktory", "gdzie", "jest", "jeszcze", "nie"} Sub Main() Dim open_dialog As New OpenFileDialog() open_dialog.InitialDirectory = "c:\" open_dialog.Filter = "All Files|*.*" If open_dialog.ShowDialog() = System.Windows.Forms.DialogResult.OK Then 'pobiera tekst do zmiennej wiadomosc = IO.File.ReadAllText(open_dialog.FileName) Console.WriteLine("potencjalne klucze to: ") Dim klucz As Char For j As Integer = 0 To 127 klucz = Chr(j) wiadomoscOdszyfrowana = "" Dim z As Integer = Asc(klucz) For i As Int32 = 0 To wiadomosc.Length - 1 Dim y As Integer = Asc(wiadomosc(i)) If ((y - z) Mod 127) < 0 Then wiadomoscOdszyfrowana += Chr(127 + ((y - z) Mod 127)) Else wiadomoscOdszyfrowana += Chr(((y - z) Mod 127)) End If z = (127 + ((y - z) Mod 127)) Next Dim iloscZawartychslow As Integer = 0 For i As Integer = 0 To slownik.Length - 1 If wiadomoscOdszyfrowana.Contains(slownik(i)) Then If Not listaKluczy.Contains(klucz) Then listaKluczy.Add(klucz) End If iloscZawartychslow += 1 End If Next If iloscZawartychslow > 0 Then Console.WriteLine(klucz.ToString + " (" + _ Math.Round((iloscZawartychslow / slownik.Length) * 100, 2).ToString + "% słownika)") End If Next Console.ReadLine() End If End Sub End Module |
Efekt:
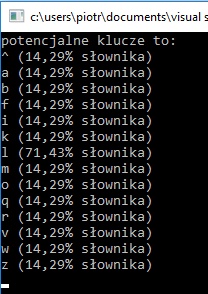
Nie muszę wam chyba mówić jaką literę użyłem w autokluczu. Im dłuższy będzie nasz słownik, tym więcej kluczy może się pojawić, ale również ilość odnalezionych słów słownika może być większa, co oznacza, że skuteczność analizy będzie wyższa.
Były rzeczy proste, teraz przejdźmy do czegoś trudniejszego. Co by było gdybyśmy chcieli znaleźć klucz na siłę, sprawdzając wszystkie dostępne możliwości. Zobaczmy jak by to wyglądało:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 |
Imports System.Windows.Forms Module Module1 Dim wiadomosc As String Dim wiadomoscOdszyfrowana As String Dim listaKluczy As New List(Of Char) Dim slownik() As String = {"ale", "do", "ktory", "gdzie", "jest", "jeszcze", "nie", "kto", "ten", "to", "dla", "ma", "bez", "jej", "jego", "bo"} Dim listamozliwosia(127) As Integer Dim startTime As DateTime Sub Main() Dim open_dialog As New OpenFileDialog() open_dialog.InitialDirectory = "c:\" open_dialog.Filter = "All Files|*.*" For i As Integer = 0 To 127 listamozliwosia(i) = i Next If open_dialog.ShowDialog() = System.Windows.Forms.DialogResult.OK Then 'pobiera tekst do zmiennej wiadomosc = IO.File.ReadAllText(open_dialog.FileName) Do Console.Write("Jak długi klucz chcesz sprawdzić:") Dim dlugoscKlucza As Integer = Console.ReadLine() Dim tablica(dlugoscKlucza - 1)() As Integer For y As Integer = 0 To tablica.Length - 1 tablica(y) = listamozliwosia Next startTime = DateTime.Now Console.WriteLine("Zaczęto: " + DateTime.Now.ToString("yyyy/MM/dd HH:mm:ss")) 'przykła użycia metody wszystkich permutacji CartesianProduct(tablica) Console.WriteLine("Ukończono: " + DateTime.Now.ToString("yyyy/MM/dd HH:mm:ss")) Dim endtimeTime = DateTime.Now Console.WriteLine("Trwało to: " + (endtimeTime - startTime).ToString) Console.WriteLine("Chcesz sprawdzić inne klucze? (t/n)") If Console.ReadLine().ToLower = "n" Then Exit Do End If Loop Console.ReadLine() End If End Sub Dim zliczacz As Long = 0 Private Sub CartesianProduct(Of T)(ParamArray sequences As T()()) Dim result As IEnumerable(Of Integer()) = {New Integer() {}} For Each sequence As Array In sequences Dim s = sequence result = From seq In result, item In s Select seq.Concat({item}).ToArray() Next For Each seq In result Dim mojklucz(seq.Length - 1) As Integer For i As Integer = 0 To seq.Length - 1 mojklucz(i) = seq(i) Next Dim wiadomoscOdszyfrowana As String = "" For i As Integer = 0 To wiadomosc.Length - 1 Dim k As Integer = Asc(wiadomosc(i)) Dim test As Integer = (k - mojklucz(i Mod mojklucz.Length) Mod 127) If test < 0 Then wiadomoscOdszyfrowana += Chr(127 + test) Else wiadomoscOdszyfrowana += Chr(test) End If Next 'pętla sprawdza potencjalne klucze czy po przestawieniu zawierają słowa ze słownika Dim iloscZawartychslow As Integer = 0 For i As Integer = 0 To slownik.Length - 1 If wiadomoscOdszyfrowana.Contains(slownik(i)) Then iloscZawartychslow += 1 End If Next If iloscZawartychslow / slownik.Length * 100 > 30 Then Dim klucza As String = "" Dim klucza2 As String = "" For i As Integer = 0 To mojklucz.Length - 1 klucza += Chr(mojklucz(i)) klucza2 += mojklucz(i).ToString + "," Next Dim StoptimeTime = DateTime.Now Console.WriteLine(" " + klucza + " (" + klucza2 + ") " + (iloscZawartychslow / slownik.Length * 100).ToString + "% po " _ + (StoptimeTime - startTime).ToString) End If Console.SetCursorPosition(0I, Console.CursorTop) Console.Write(zliczacz.ToString) zliczacz += 1 Next End Sub End Module |
Czas w jakim program znalazł klucz „cba” wynosił u mnie:
Sprawdzenie wszystkich możliwości trwało u mnie 14 minut. Czy to dużo? Zależy, nie mam za dobrego komputera więc u was może to potrwać krócej. mój komputer sprawdził 127*127*127= 2 048 383 możliwych kombinacji w 14 minut. Ile czasu potrwało by złamanie dłuższego klucza:
klucz czteroliterowy: 14,92 min *127 = 1894,84 min /60=31 godzin 34 minuty i 50 sekund
klucz pięcioliterowy: 1894,84 min *127 =240 644,68 minut = 167 dni 6 godzin 51 minut 41 sekund
Kiedy użyłem rozszerzonego słownika, dostałem więcej propozycji klucza:
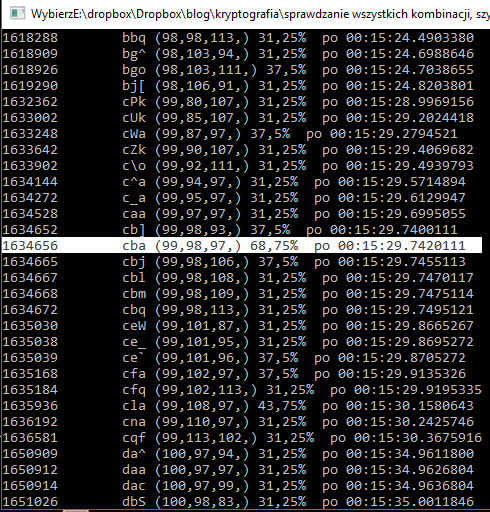
To tak rośnie i rośnie, jak widzicie mało efektywna metoda. To wszystko zakładając, że tekst zawierał tylko litery z ASCII których mamy tylko 127, zmienna typu Char ma zakres dłuższy do 255 znaków i zawiera znaki regionalne takie jak „ą”, „ć” i inne znaki regionalne. To oznacza, że jeśli zaszyfrujemy tekst na komputerze z językiem polskim i odszyfrujemy go na komputerze z językiem polskim zachowamy jego pełną formę. Aby to zrobić skorzystajcie z kodu poniżej:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 |
Imports System.Text Imports System.Windows.Forms Module Module1 Dim wiadomosc As String Dim wiadomoscZaszyfrowana As String Dim wiadomoscOdszyfrowana As String Sub Main() Dim open_dialog As New OpenFileDialog() open_dialog.InitialDirectory = "c:\" open_dialog.Title = "Szyfr z kluczem, zaszyfruj plik." open_dialog.Filter = "All Files|*.*" If open_dialog.ShowDialog() = System.Windows.Forms.DialogResult.OK Then 'pobiera tekst do zmiennej wiadomosc = IO.File.ReadAllText(open_dialog.FileName, Encoding.Default) Console.Write("Zamierzasz zaszyfrować plik. Wprowadź klucz szyfrujący: ") Dim klucz As String = Console.ReadLine() 'dzieli klucz na wartości liczbowe z tabeli IOS Dim mojklucz(klucz.Length - 1) As Integer For i As Int32 = 0 To klucz.Length - 1 Dim k As Integer = Asc(klucz(i)) mojklucz(i) = k Next 'Podstawia nowe znaki tekstu For i As Int32 = 0 To wiadomosc.Length - 1 Dim k As Integer = Asc(wiadomosc(i)) wiadomoscZaszyfrowana += Chr(((k + mojklucz(i Mod mojklucz.Length)) Mod 256)) Next Console.WriteLine(wiadomosc.ToString) Console.WriteLine() Console.WriteLine(wiadomoscZaszyfrowana.ToString) Console.WriteLine() 'roszyfrowuje znaki tekstu For i As Integer = 0 To wiadomoscZaszyfrowana.Length - 1 Dim k As Integer = Asc(wiadomoscZaszyfrowana(i)) If (k - mojklucz(i Mod mojklucz.Length) Mod 256) < 0 Then wiadomoscOdszyfrowana += Chr(256 + ((k - mojklucz(i Mod mojklucz.Length)) Mod 256)) Else wiadomoscOdszyfrowana += Chr(((k - mojklucz(i Mod mojklucz.Length)) Mod 256)) End If Next Console.WriteLine((wiadomoscOdszyfrowana).ToString) 'lokalizacja zapisu zapisanego szyfru Dim LokalizacjaZapisu As String = "C:\Users\piotr\Desktop\" Console.Write("Wprowadź nazwę pliku zaszyfrowanego: ") Dim NazwaPliku As String = Console.ReadLine() Try Dim sw As New IO.StreamWriter(LokalizacjaZapisu + NazwaPliku, False, Encoding.Default) sw.Write(wiadomoscZaszyfrowana) sw.Close() Console.Write("Plik został zapisany!") Catch ex As Exception Console.Write("Problem...." + ex.ToString) End Try Console.ReadLine() End If End Sub End Module |
Zamieni on tekst jawny na szyfrogram z wpisanym kluczem i zapisuje plik na wpisanej do kodu lokalizacji. Analogicznie kod deszyfrujący:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 |
Imports System.Text Imports System.Windows.Forms Module Module1 Dim wiadomoscZaszyfrowana As String Dim wiadomoscOdszyfrowana As String Sub Main() Dim open_dialog As New OpenFileDialog() open_dialog.InitialDirectory = "c:\" open_dialog.Title = "Wskaż zaszyfrowany tekst" open_dialog.Filter = "All Files|*.*" If open_dialog.ShowDialog() = System.Windows.Forms.DialogResult.OK Then 'pobiera tekst do zmiennej wiadomoscZaszyfrowana = IO.File.ReadAllText(open_dialog.FileName, Encoding.Default) Console.Write("Wprowadź klucz szyfrujący: ") Dim klucz As String = Console.ReadLine() Dim mojklucz(klucz.Length - 1) As Integer For i As Int32 = 0 To klucz.Length - 1 Dim k As Integer = Asc(klucz(i)) mojklucz(i) = k Next For i As Integer = 0 To wiadomoscZaszyfrowana.Length - 1 Dim k As Integer = Asc(wiadomoscZaszyfrowana(i)) If (k - mojklucz(i Mod mojklucz.Length) Mod 256) < 0 Then wiadomoscOdszyfrowana += Chr(256 + ((k - mojklucz(i Mod mojklucz.Length)) Mod 256)) Else wiadomoscOdszyfrowana += Chr(((k - mojklucz(i Mod mojklucz.Length)) Mod 256)) End If Next Console.WriteLine((wiadomoscOdszyfrowana).ToString) 'lokalizacja zapisu zapisanego szyfru Dim LokalizacjaZapisu As String = "C:\Users\piotr\Desktop\" Console.Write("Wprowadź nazwę pliku zaszyfrowanego: ") Dim NazwaPliku As String = Console.ReadLine() Dim sw As New IO.StreamWriter(LokalizacjaZapisu + NazwaPliku, False, Encoding.Default) sw.Write(wiadomoscOdszyfrowana) sw.Close() Console.ReadLine() End If End Sub End Module |
Jakie więc kroki podjąć aby nasz zaszyfrowany tekst nie sprawdzać przez pół roku. Zaszyfrowałem dosyć długi tekst, jest to recenzja pewnej gry, do pobrania poniżej:
Nie zdradzę wam ani klucza ani jego długości, ale powiem jakie kroki należy podjąć aby go wydobyć z tekstu. Najpierw poznamy długość klucza, z góry zakładamy, że klucz jest dłuższy niż 3 litery. Użyjemy testu Kasiskiego:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 |
Imports System.Windows.Forms Module Module1 Dim wiadomosc As String Dim dlugoscKlucza As Integer Sub Main() Dim open_dialog As New OpenFileDialog() open_dialog.InitialDirectory = "c:\" open_dialog.Title = "Który szyfrogram chcesz analizować" open_dialog.Filter = "All Files|*.*" If open_dialog.ShowDialog() = System.Windows.Forms.DialogResult.OK Then 'pobiera tekst do zmiennej wiadomosc = IO.File.ReadAllText(open_dialog.FileName) Console.Write("Od jakiej długości klucza chcesz zacząć?:") Dim DlugosciKluczyStart As Integer = Console.ReadLine() Console.Write("Na jakiej długości kluczy chcesz skończyć?:") Dim DlugosciKluczyKoniec As Integer = Console.ReadLine() For k As Integer = DlugosciKluczyStart To DlugosciKluczyKoniec Dim listaSekwencji As New List(Of List(Of String)) dlugoscKlucza = k Console.WriteLine(">>>>> Klucz o długości '{0}' posiada powtarzające się sekwencje:", k) For i As Integer = 0 To wiadomosc.Length - (1 + (wiadomosc.Length Mod dlugoscKlucza)) _ Step dlugoscKlucza Dim zawiera As Boolean = False Dim sekwencja As String = "" Dim sekwencjaASCII As String = "" For j As Integer = i To i + dlugoscKlucza - 1 sekwencja += wiadomosc(j).ToString + "," Next For j As Integer = 0 To listaSekwencji.Count - 1 If listaSekwencji(j).Contains(sekwencja) Then listaSekwencji(j).Add(sekwencja) zawiera = True Exit For End If Next If zawiera = False Then Dim znak As New List(Of String) znak.Add(sekwencja) listaSekwencji.Add(znak) End If Next listaSekwencji.Sort(Function(L1 As List(Of String), L2 As List(Of String)) _ (L2.Count).CompareTo(L1.Count)) For i As Int32 = 0 To listaSekwencji.Count - 1 If listaSekwencji(i).Count > 1 Then Dim tablica() As String = listaSekwencji(i)(0).Split(",") Dim Cyfry As String = "" For r As Integer = 0 To tablica.Length - 2 Dim str As String = Asc(tablica(r)).ToString Cyfry += str + "," Next Cyfry = Cyfry.Substring(0, Cyfry.Length - 1) Console.WriteLine(vbTab + listaSekwencji(i)(0).ToString + " (" + Cyfry + ") znaleziono sekwencji:" + listaSekwencji(i).Count.ToString) End If Next Next Console.ReadLine() End If End Sub End Module |
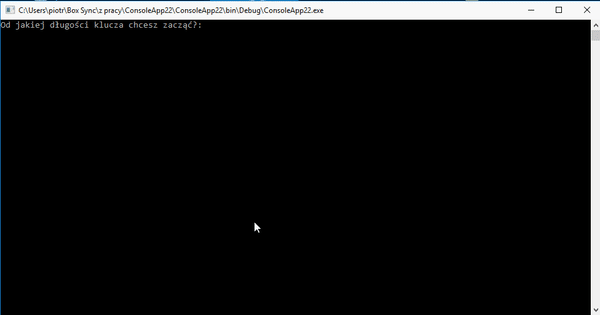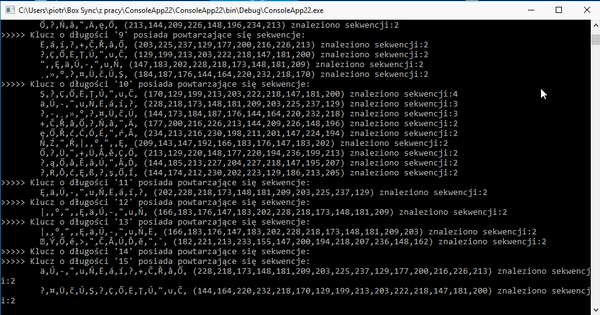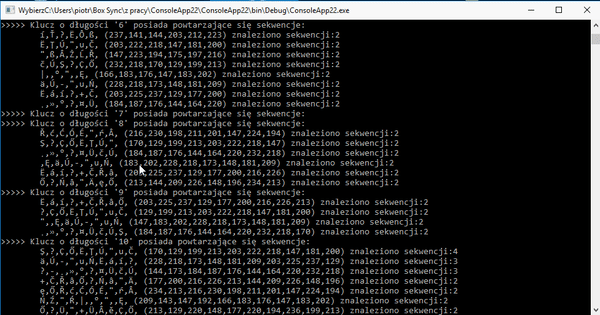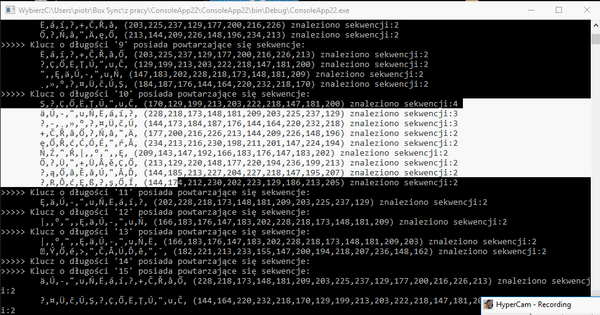Test ten pomoże nam poznać długość klucza. Ponieważ szyfrogram posiada najwięcej sekwencji dla klucza 4, 5 i 10 literowego można gdybać, że klucz jest właśnie tej długości, oczywiście jest to trochę wyidealizowany scenariusz. Następnym krokiem jest sprawdzanie najczęściej występujących znaków. Nie będziemy tutaj sprawdzać 4 i 10 ponieważ klucz jest 5 literowy więc nie przedłużając będziemy rozpatrywać klucz 5 literowy.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 |
Imports System.Windows.Forms Module Module1 Dim wiadomosc As String Dim listZnakow As New List(Of List(Of Char)) Dim dlugoscKlucza As Integer Dim literaKlucza As Integer Dim tekst As String Sub Main() Dim open_dialog As New OpenFileDialog() open_dialog.InitialDirectory = "c:\" open_dialog.Filter = "All Files|*.*" If open_dialog.ShowDialog() = System.Windows.Forms.DialogResult.OK Then 'pobiera tekst do zmiennej wiadomosc = IO.File.ReadAllText(open_dialog.FileName) Console.Write("Jak długi jest klucz? :") dlugoscKlucza = Console.ReadLine() Do Console.Write("Którą pozycje klucza chcesz sprawdzić:") literaKlucza = Console.ReadLine() For i As Integer = 0 To wiadomosc.Length - (1 + literaKlucza) If (i Mod dlugoscKlucza) = literaKlucza Then Dim zawiera As Boolean = False tekst += wiadomosc(i) For j As Integer = 0 To listZnakow.Count - 1 If listZnakow(j).Contains(wiadomosc(i)) Then listZnakow(j).Add(wiadomosc(i)) zawiera = True Exit For End If Next If zawiera = False Then Dim znak As New List(Of Char) znak.Add(wiadomosc(i)) listZnakow.Add(znak) End If End If Next Dim wiadomoscZaszyfrowana As String = "" For i As Integer = 0 To wiadomosc.Length - 1 wiadomoscZaszyfrowana += wiadomosc(i) Next Console.WriteLine(wiadomoscZaszyfrowana) Console.WriteLine() Console.WriteLine(tekst) Console.WriteLine() listZnakow.Sort(Function(L1 As List(Of Char), L2 As List(Of Char)) _ (L2.Count).CompareTo(L1.Count)) For i As Int32 = 0 To listZnakow.Count - 1 Console.WriteLine(listZnakow(i)(0) + " stanowi:" + (Math.Round(listZnakow(i).Count / tekst.Length, 4) * 100).ToString + " % kod ASCII znaku:" + Asc(listZnakow(i)(0)).ToString) Next Console.WriteLine("Chcesz sprawdzić inne pozycje? (tak/nie)") If Console.ReadLine().ToLower = "nie" Then Exit Do End If Loop Console.ReadLine() End If End Sub End Module |
Jak to robimy? Sprawdzamy litery na każdej pozycji, zaczynając od 0 na 4 kończąc.
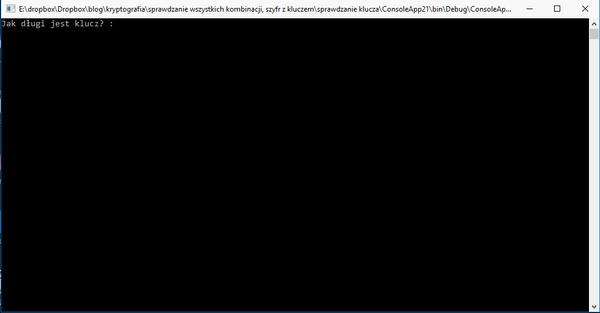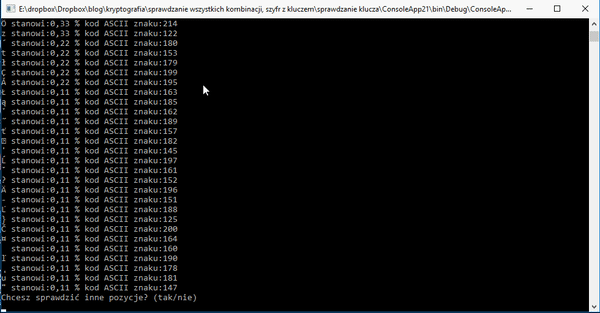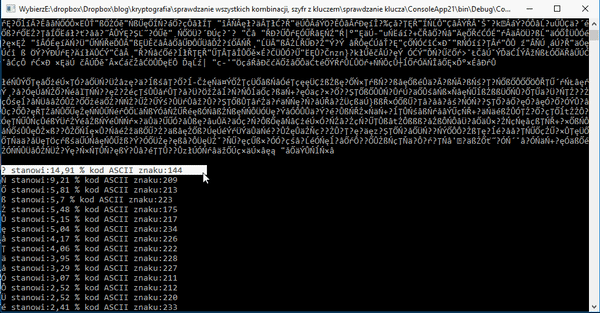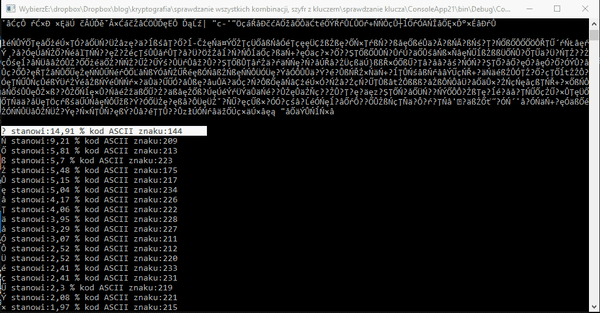
Przeprowadzamy test dla każdej pozycji klucza. Kiedy to zrobimy, mamy potencjalny trop. Kolejny kod jest bardzo podobny do tego sprawdzającego wszystkie permutacje. Pętla jednak nie sprawdza wszystkich dostępnych możliwości, działa na tablicach stworzonych przez użytkownika. Jak to będzie wyglądać?.
Im więcej liter sprawdzimy tym nasz zbiór wejściowy będzie dłuższy, ja będę szukał tylko dwóch liter ale na dużych zbiorach.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 |
Imports System.Windows.Forms Module Module1 Dim wiadomosc As String Dim slownik() As String = {"ale", "do", "ktory", "gdzie", "jest", "jeszcze", "nie", "kto", "ten", "to", "dla", "ma", "bez", "jej", "jego", "bo"} Dim startTime As DateTime Sub Main() Dim open_dialog As New OpenFileDialog() open_dialog.InitialDirectory = "c:\" open_dialog.Title = "Wskaż szyfrogram." open_dialog.Filter = "All Files|*.*" If open_dialog.ShowDialog() = System.Windows.Forms.DialogResult.OK Then 'pobiera tekst do zmiennej wiadomosc = IO.File.ReadAllText(open_dialog.FileName) Do Console.Write("Jak długi klucz chcesz sprawdzić:") Dim dlugoscKlucza As Integer = Console.ReadLine() Console.Write("Podaj litery na podstawie którychc chcesz sprawdzic szyfr, oddzielajając je przecinkiem:") Dim listaLiter() As String = Console.ReadLine().Split(",") Dim listaLiterasc(listaLiter.Length - 1) As Integer For i As Integer = 0 To listaLiter.Count - 1 listaLiterasc(i) = Asc(CChar(listaLiter(i))) Next Dim tablica(dlugoscKlucza - 1)() As Integer For y As Integer = 0 To tablica.Length - 1 Console.Write("Podaj tablice numerów ASC najczęsciej występujących na pozycji {0}:", y) Dim NumeryASCNajczesciejwystepujace() As String = Console.ReadLine().Split(",") Dim Wartosciasc As New List(Of Integer) For i As Integer = 0 To NumeryASCNajczesciejwystepujace.Count - 1 For j As Integer = 0 To listaLiterasc.Length - 1 Dim test As Integer = CInt(NumeryASCNajczesciejwystepujace(i)) - listaLiterasc(j) If test < 0 Then Wartosciasc.Add(256 + test) Else Wartosciasc.Add(test) End If Next Next tablica(y) = Wartosciasc.ToArray Next startTime = DateTime.Now Console.WriteLine("Zaczęto: " + DateTime.Now.ToString("yyyy/MM/dd HH:mm:ss")) CartesianProduct(tablica) Console.WriteLine() Console.WriteLine("Ukończono: " + DateTime.Now.ToString("yyyy/MM/dd HH:mm:ss")) Dim endtimeTime = DateTime.Now Console.WriteLine("Trwało to: " + (endtimeTime - startTime).ToString) Console.WriteLine("Chcesz sprawdzić inne klucze? (tak/nie)") If Console.ReadLine().ToLower = "nie" Then Exit Do End If Loop Console.ReadLine() End If End Sub Dim zliczacz As Long = 0 Private Sub CartesianProduct(Of T)(ParamArray sequences As T()()) Dim result As IEnumerable(Of Integer()) = {New Integer() {}} For Each sequence As Array In sequences Dim s = sequence result = From seq In result, item In s Select seq.Concat({item}).ToArray() Next For Each seq In result Dim mojklucz(seq.Length - 1) As Integer For i As Integer = 0 To seq.Length - 1 mojklucz(i) = seq(i) Next Dim wiadomoscOdszyfrowana As String = "" For i As Integer = 0 To wiadomosc.Length - 1 Dim k As Integer = Asc(wiadomosc(i)) Dim test As Integer = (k - mojklucz(i Mod mojklucz.Length) Mod 256) If test < 0 Then wiadomoscOdszyfrowana += Chr(256 + test) Else wiadomoscOdszyfrowana += Chr(test) End If Next Dim iloscZawartychslow As Integer = 0 For i As Integer = 0 To slownik.Length - 1 If wiadomoscOdszyfrowana.Contains(slownik(i)) Then iloscZawartychslow += 1 End If Next If iloscZawartychslow / slownik.Length * 100 > 50 Then Dim klucza As String = "" Dim klucza2 As String = "" For i As Integer = 0 To mojklucz.Length - 1 klucza += Chr(mojklucz(i)) klucza2 += mojklucz(i).ToString + "," Next Dim StoptimeTime = DateTime.Now Console.WriteLine(" " + klucza + " (" + klucza2 + ") " + (iloscZawartychslow / slownik.Length * 100).ToString + "% po " + (StoptimeTime - startTime).ToString) End If Console.SetCursorPosition(0I, Console.CursorTop) Console.Write(zliczacz.ToString) zliczacz += 1 Next End Sub End Module |
Warto zaznaczyć tutaj, że w niektórych przypadkach litera stanowiła 14% albo 9% wtedy możemy te zbiory ograniczyć ponieważ to może być litera „a”. Mój test:
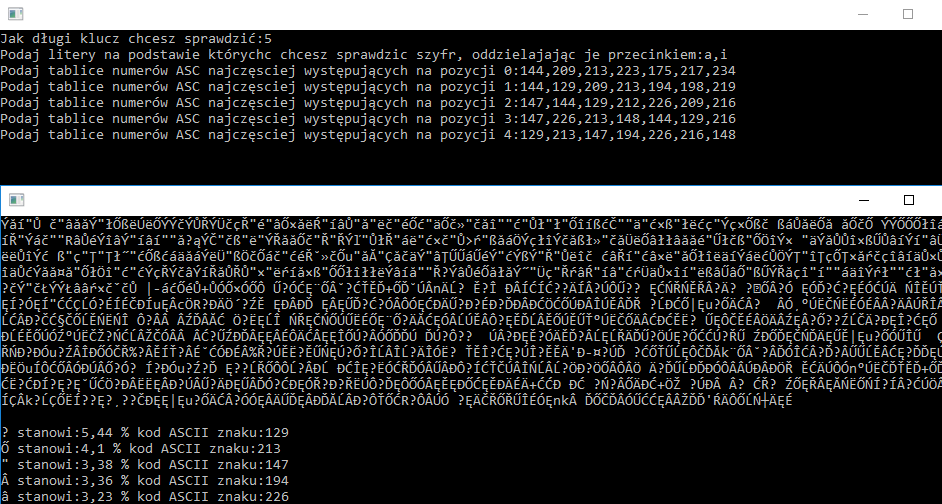
Ilość kombinacji = (7*2)*(7*2)*(7*2)*(7*2)*(7*2)= 537 824. Jeśli nawet założyliśmy błędne zbiory, a klucz ma 10 lub 15 liter, to i tak w wypadku gdy trzy litery obok siebie tworzą słowo ze słownika, przy następnej analizie ich zbiory można ograniczyć a zbiory liter nietrafionych poszerzyć. Kod powyżej wyłapuje tylko te sekwencje klucza, które zawierają więcej niż 50% słów ze słownika, można tą wartość zmniejszyć, co ułatwi poszukiwanie liter w mniejszych zbiorach. Mój test:
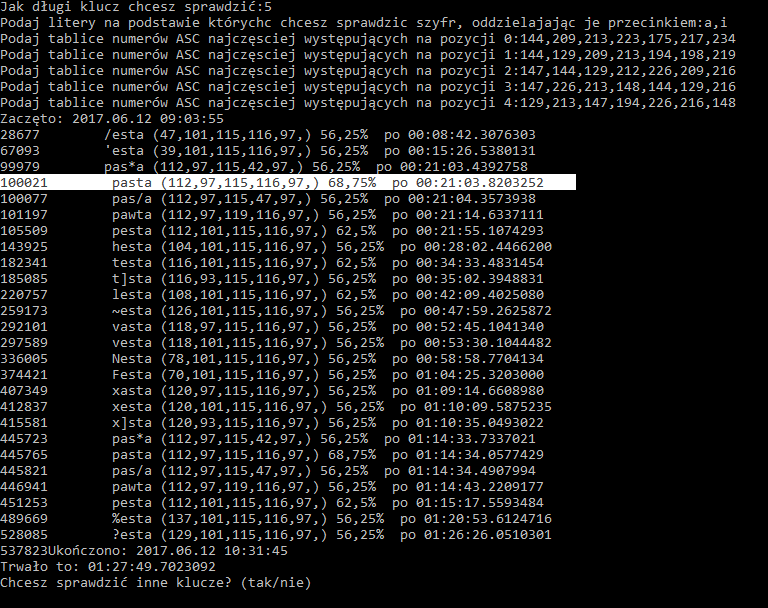
Klucz się powtarza, ponieważ zapewne we wszystkich zbiorach znajdowała się litera „a” i „i”, test trwał nie kilka dni a 1,5 godziny, ale odpowiedź była już po 21 minutach. Jak widzicie jedna sekwencja powtarza się często, jest to „sta” można to w prosty sposób wykorzystać.
Jeśli założymy, że ostatnia litera jest „a” to trzeba wyodrębnić literę a ze zbioru czyli:
ASC(„a”)+(ASC(„a”) lub ASC(„i”))= 97+97 =194
ASC(„t”)+(ASC(„a”) lub ASC(„i”)) = 116 +97 =213
ASC(„s”)+(ASC(„a”) lub ASC(„i”)) =115+97=212
Wtedy nasz klucz zostanie znaleziony w kilka sekund:
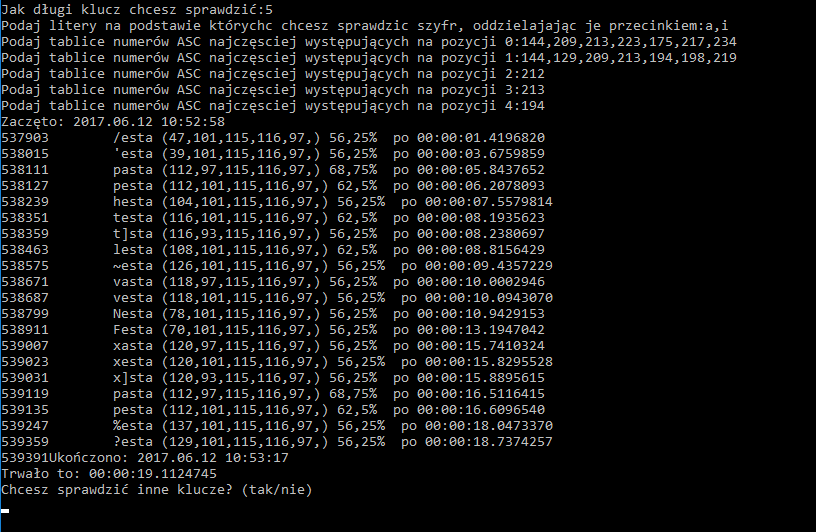
Taką metodę można zastosować w przypadku długich kluczy. Jeśli gdzieś w kluczu powtarza się jakaś sekwencja i łapie ona słowo ze słownika takie jak „albo”, „lub”, „kto”, można przypuszczać, że ten element klucza został rozszyfrowany.
