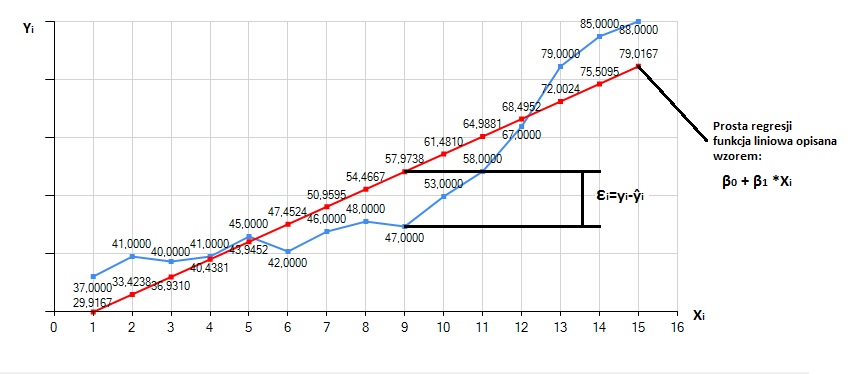
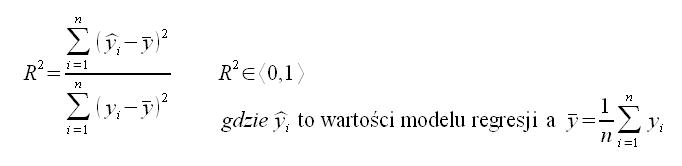Kolejnym etapem w naszej podróży po prognozowaniu będą modele regresji liniowej. Model ten polega na dopasowaniu takiego wzoru funkcji liniowej, dla którego każdy element obserwacji będzie miał najmniejszą możliwą odległość od prostej regresji. Wzór modelu wygląda następująco:

gdzie:

Y – Zmienna objaśniana.

X – zmienna objaśniająca.

β1 i β0 – parametry strukturalne.

ε – Składnik losowy.

Jak można zauważyć, model ten składa się głównie z funkcji liniowej (gdy X jest stale rosnącą zmienną czasu, funkcję taką nazywamy liniową) i składnika losowego. Na wykresie wygląda to dużo jaśniej:

Aby wyznaczyć przybliżone wartości parametrów β1≈b1 i β0≈b0 stosuje się metodę najmniejszych kwadratów. Najpierw musimy wyznaczyć minimum funkcji

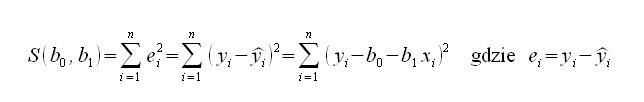Następnie po przekształceniu wzory wyliczamy pochodne dla

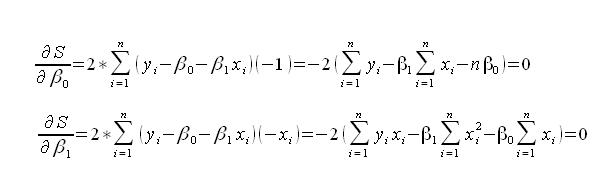Po przekształceniu ostatecznie uzyskujemy wzór na obliczenie przybliżonych parametrów b1 i b0.

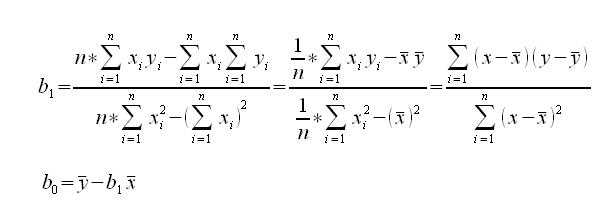
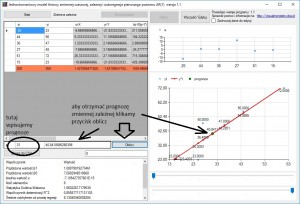
Jak wygląda to w praktyce: Dla parametrów: 37,41,40,41,45,42,46,48,47,53,58,67,79,85,88 wyznaczyć prostą regresji. Posłużymy się programem stworzonym do obliczania prostej regresji. Aby to zrobić odpalamy program dostępny tutaj: jednorownaniowe-mode-liniowe

Wybieramy „Start” następnie z kilku opcji wybieramy „Zmienna czasowa”

Kopiujemy dane, zaznaczając i klikając jednocześnie Ctrl+C. następnie w oknie programu wciskamy jednocześnie Ctrl+V. Program powinien zapytać się o rodzaj użytego separatora. Jeśli skopiowaliście dane z tej strony, jako separator należy wybrać „,”: Dane można też po prostu przepisać ze strony.

Nasze dane powinny pojawić się w oknie po lewej stronie. Po kliknięciu przycisku „Oblicz” wszystko powinno zostać obliczone:

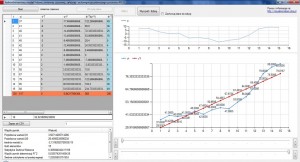W oknie po lewej stronie mamy różne rodzaje obliczeń a na samym dole podkreślone na pomarańczowo sumy poszczególnych kolumn.

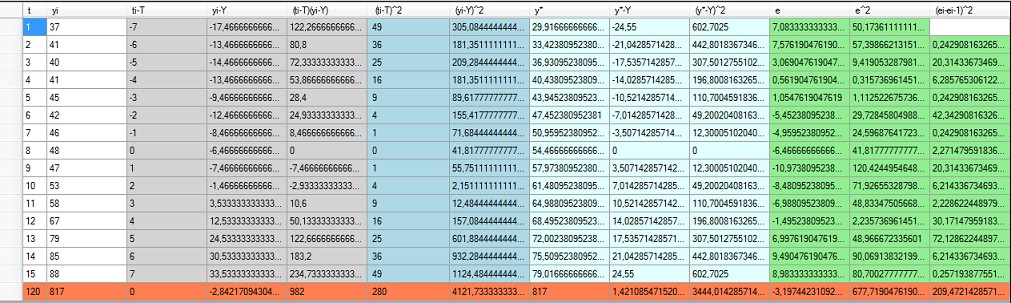Po obliczeniu nasze parametry przyjmują wartości:

Naszą prosta regresji określa wzór:

Y= 3,50714285714286*t + 26,4095238095238

Przydatność danego modelu określamy za pomocą miar dopasowania. Jedną z takich miar jest:

Wariancja reszt. Jest to uśrednienie pól kwadratów zbudowanych na resztach i odzwierciedla stopień dopasowania prostej regresji do danych statystycznych. Wyrażamy ją wzorem.

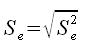 oznacza średnie (standardowe) odchylenie od prostej regresji.

Najprostszą względną miarą dopasowania jest współczynnik zmienności losowej który określamy wzorem

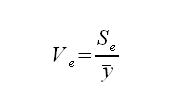Współczynnik ten informuje jaką część średniej wartości badanego zjawiska stanowi odchylenie standardowe reszt. Mniejsze wartości tego współczynnika wskazują na lepsze dopasowanie modelu do danych empirycznych. Niekiedy żąda się, aby współczynnik ten nie przekraczał 20% lub 30 %.

Miarą dopasowania modelu do wartości zaobserwowanych jest również współczynnik determinacji

Współczynnik ten określa jaką część całkowitej zmienności zmiennej objaśnianej została wyjaśniona przez model regresji liniowej. Można ją podawać w procentach na przykład, gdy R^2=0,82 mówimy „rozpatrywany model wyjaśnia 82% całkowitej wielkości produkcji mleka”.

Ostatnią bardzo istotną miarą dopasowania jest Statystyka Durbina-Watsona. Służy ona do testowania korelacji reszt następujących po sobie w szeregu czasowym. Określamy ją wzorem:

Statystyka ta może przyjmować wartości od 0 do 4. Wartości bliskie zeru świadczą o bardzo silnej dodatniej autokorelacji, wartość 2 oznacza brak autokorelacji, natomiast wartości bliskie 4 o silnej ujemnej autokorelacji. Podczas wyznaczania modelu regresji liniowej oczekujemy, że wartość tego współczynnika będzie bardzo blisko wartości 2, inna wartość będzie oznaczała, że do prognozowania warto użyć modelu autoregresji.

 Model Autoregresji

Tworzymy za pomocą zastąpienia zmiennej czasowej t wartościami yi-1, wygląda to tak jak na obrazku:

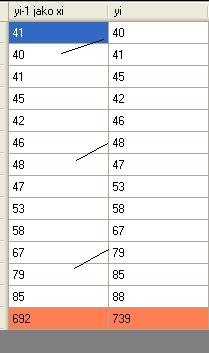Na takiej podstawie zmiennych budowany jest model regresji nazywany modelem autoregresji AR(1). Jest to model bardzo skuteczny, ponieważ dane objaśniające nie są jednostką czasu kiedy rozwijała się objaśniana a sama objaśniana. To powoduje dużo lepsze dopasowanie modelu regresji do naszych zmiennych i pozwala na wyznaczenie skutecznej prognozy. Wykres takiego modelu wygląda następująco:

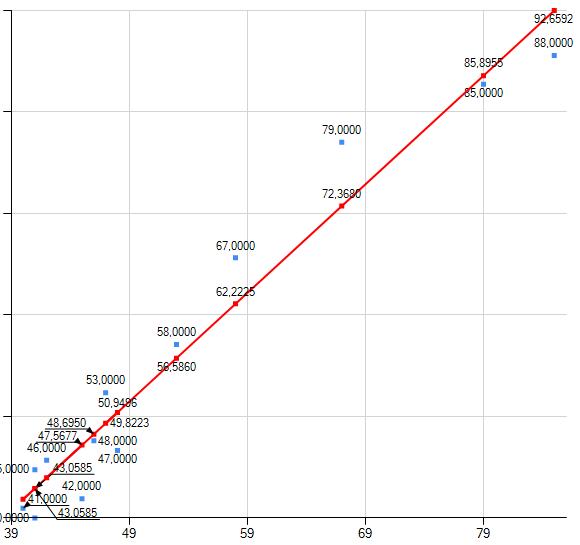Jak widzimy dane znajdują się w dość bliskim sąsiedztwie naszej prostej regresji.

Również miary dopasowania są dużo bardziej optymistyczne:

Korelacja liniowa

Program oferuje również możliwość obliczanie modelu regresji dla zmiennych zależnych. Kiedy chcemy np. obliczyć zależność kosztów do wielkości produkcji. Przykład:

xi = { 25,44,36,27,61,15} yi= {23,56,47,48,72,23}

Po wprowadzeniu tych danych do programu dostajemy:

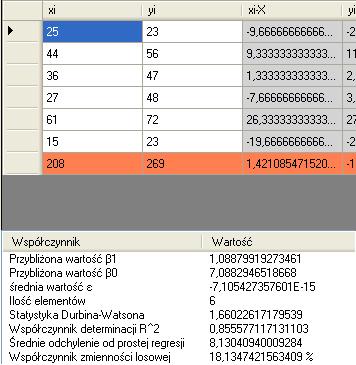Osiągnięty model ma sens tylko wtedy gdy znamy przyszłą wartość xi tzn jeśli założymy, że koszty produkcji na następny okres czasu wyniosą 31 tysięcy. Wtedy wykorzystując nasz model regresji możemy obliczyć przyszło wielkość produkcji.

Y*= 31 * 1,08879919273461 + 7,0882946518668

Przyszła wielkość produkcji przy założonych kosztach produkcji 31 tysięcy wyniesie po zaokrągleniu  41 tysięcy sztuk ± 8 tysięcy.

W programie wygląda to tak: