W kryptografii często używa się liczb pierwszych, wykorzystuje się ich specyficzne właściwości, które są nieocenione w nowoczesnej kryptografii. W podstawowym artykule do szyfrowania używaliśmy dodawania i odejmowania, poprzez zmianę pozycji litery w słowniku, używaliśmy dodawania i odejmowania, ponieważ po ich użyciu otrzymywaliśmy liczby całkowite. Innym operatorem, który po użyciu również daje liczbę całkowitą, jest mnożenie. Jednak jego wykorzystanie jest dużo bardziej kłopotliwe. Przypuśćmy że chcemy zaszyfrować wartość 54 przy użyciu szyfru *12 (mnożenie razy 12)
54 = (54 * 12) mod 256 =648 mod 256 = 2*256 + 136 = 136 wartość zaszyfrowana *12
Czy takie szyfrowanie jest skuteczne? Spróbujmy odwrócić szyfr z kryptogramu. Wiemy że szyfr jest *12 i znamy rezultat szyfrowania którym jest 136
(x*12) mod 256 = 136 || 12x -(256*y) = 136 || y=(12x-136)/256
Oczywiste jest, że x przyjmuje wartości, od 0 do 255 a y należy do zbioru liczb całkowitych, tak więc sprawdzając odpowiedzi prostym algorytmem:
|
|
Module Module1 Sub Main() For X As Integer = 0 To 255 Dim Y As Double = (12 * X - 136) / 256 'sprawdza czy liczba jest całkowita If Y = Int((12 * X - 136) / 256) Then Console.WriteLine(X.ToString) End If Next Console.ReadLine() End Sub End Module |
Algorytm wskazuje, że nasza liczba x może być liczbą (54,118, 182, 246) Sprawdźmy więc
246 || (246*12) mod 256 = 2952 mod 256 = 11*256 +136 =136
182 || (182*12) mod 256 = 2184 mod 256 = 8*256 +136 =136
118 || (118*12) mod 256 = 1416 mod 256 = 5*256 +136 =136
54 || (54*12) mod 256 = 648 mod 256 = 2*256 +136 =136
Nasz wzór ma wiele rozwiązań, co wiąże się z tym, że zaszyfrowanie nim wartości 246, 182, 118 po odszyfrowaniu da wartość najniższą 54. Sprawdźmy co się jednak stanie, gdy użyjemy do przesunięcia liczby pierwszej? Czy odwrócenie reszty z dzielenia da w odpowiedzi wiele rozwiązań? Użyjmy prostej liczby pierwszej *11
54 = (54 * 11) mod 256 =594 mod 256 = 2*256 + 82 = 82 wartość zaszyfrowana *12
y=(11x-82)/256
|
|
Module Module1 Sub Main() For X As Integer = 0 To 255 Dim Y As Double = (11 * X - 82) / 256 If Y = Int((11 * X - 82) / 256) Then Console.WriteLine(X.ToString) End If Next Console.ReadLine() End Sub End Module |
Algorytm wskazuje, że naszą liczbą x może być tylko liczba 54. Co więcej, nie ma skutecznego wzoru na obliczanie liczby pierwszej (mimo iż odkryto już bardzo wielkie liczby pierwsze). Mimo iż liczb pierwszych jest ograniczona ilość (tych znanych), jest ich wystarczająco dużo, aby skutecznie zaszyfrować wiadomość, co więcej, kiedy zaszyfrujemy wiadomość lub obrazek przy pomocy dodawania, lub odejmowania zachowujemy ich pierwotny rozkład wartości, który jest zwiększony, lub zmniejszony, łatwo wtedy określić długość klucza szyfrującego sprawdzając, czy taki rozkład ma stałą amplitudę zmian sezonowych. Aby usunąć ten problem, należy pozbyć się tej amplitudy, poprzez mnożenie wartości klucza/indeksu, nie da się więc tak łatwo, poznać długości klucza co komplikuje sprawę. Najlepiej widać to podczas szyfrowania obrazków, wybierzmy sobie jakąś liczbę pierwszą, np. 139:
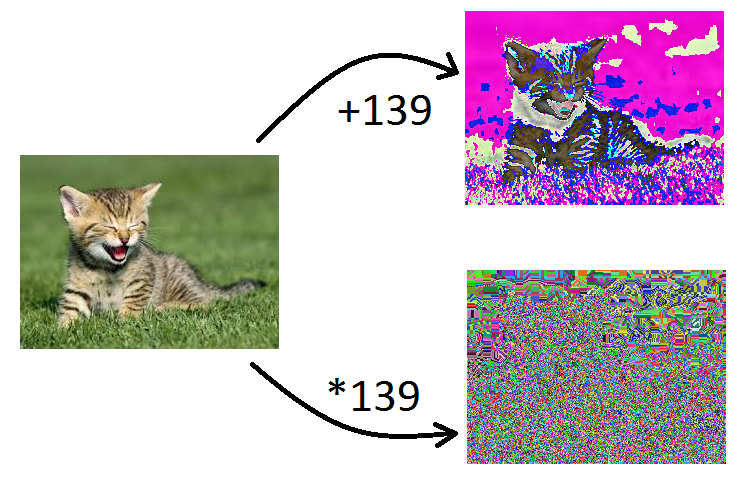
Widać różnicę gołym okiem. Spowodowane jest to tym, że wszystkie wartości na pierwszym obrazku zostały zamienione na wartości o x razy większe, a wartości w obrazku drugim wartości nie zostały zwiększone ani zmniejszone, one zostały podmienione na wartości wynikające z działania odpowiedniej funkcji. Wartości w drugim obrazku nie są w żaden sposób ze sobą powiązane, jak to bywa w obrazku pierwszym. Jeśli weźmiemy wartości kolorów:
| kolor |
Obrazek +139 |
Obrazek *139 |
| (203,205,207) |
(203+139) mod 256 = 87
(205+139) mod 256 = 89
(207+139) mod 256 = 91 |
(203*139) mod 256 = 57
(205*139) mod 256 = 79
(207*139) mod 256 = 101 |
Mimo iż kolory w +139 nie są identyczne ich odcień został zachowany, ich zależność wewnętrzna i zewnętrzna (w skali całego obrazka) została zachowana. Zależność ta przy działaniu *139 została zaburzona i otrzymaliśmy kolor o innym odcieniu i barwie.
Przykładowy algorytm szyfrujący tą metodą:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 |
Imports System.Windows.Forms Imports System.Drawing Module Module1 Dim lokalizacjaPlikuGraficznego As String Sub Main() Dim open_dialog As New OpenFileDialog() open_dialog.InitialDirectory = "c:\" open_dialog.Filter = "Image Files (*.jpeg; *.png; *.bmp)|*.jpg; *.png; *.bmp" If open_dialog.ShowDialog() = System.Windows.Forms.DialogResult.OK Then lokalizacjaPlikuGraficznego = open_dialog.FileName Dim bmp As New Bitmap(lokalizacjaPlikuGraficznego) Console.WriteLine("Wprowadź wartość przesunięcia dla szyfru podstawieniowego") Dim przesuniecie As Long = 0 'Czeka aż użytkownik wpisze liczbę pierwszą Do Dim test As String = Console.ReadLine() If IsNumeric(test) Then Dim twojaLiczbaJestPierwsza As Boolean = True ''algorytm sprawdza czy wpisana liczba jest pierwsza (wolna metoda) For i As Integer = 2 To Math.Ceiling(test / 2) If test Mod i = 0 Then twojaLiczbaJestPierwsza = False Exit For End If Next If twojaLiczbaJestPierwsza = True Then przesuniecie = test Exit Do Else Console.WriteLine("Twoja liczba nie jest liczbą pierwszą.") End If Else Console.WriteLine("Wprowadzona wartość nie jest liczbą.") End If Loop Dim R As Long = 0, G As Long = 0, B As Long = 0 Dim xmax As Integer = bmp.Width - 1 Dim ymax As Integer = bmp.Height - 1 Dim pixelElementIndex As Long = 0 'służy do określenia ile procent obrazu zostało zaszyfrowane Dim calkowitaIloscPx As Integer = bmp.Width * bmp.Height Dim aktualnaWartosc As Integer = 0 For y = 0 To ymax For x = 0 To xmax With bmp.GetPixel(x, y) 'podstawia wartości pod piksele R = (.R * przesuniecie) Mod 256 G = (.G * przesuniecie) Mod 256 B = (.B * przesuniecie) Mod 256 End With 'zapisuje piksel bmp.SetPixel(x, y, Color.FromArgb(R, G, B)) 'prezentuje procent postępu aktualnaWartosc += 1 Console.SetCursorPosition(0, Console.CursorTop) Console.Write((((aktualnaWartosc / calkowitaIloscPx) * 100)).ToString("00.00") & " %") Next x Next y Console.WriteLine() 'zapisuje obrazek bmp.Save("C:\Users\piotr\Desktop\" + IO.Path.GetFileNameWithoutExtension(lokalizacjaPlikuGraficznego).ToString + _ ".bmp", System.Drawing.Imaging.ImageFormat.Bmp) Console.WriteLine("Bity zostały zaszyfrowane!") Console.ReadLine() End If End Sub End Module |
Program do odszyfrowania takiego obrazka:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 |
Imports System.Windows.Forms Imports System.Drawing Module Module1 Dim lokalizacjaPlikuGraficznego As String Sub Main() Dim open_dialog As New OpenFileDialog() open_dialog.InitialDirectory = "c:\" open_dialog.Filter = "Image Files (*.jpeg; *.png; *.bmp)|*.jpg; *.png; *.bmp" If open_dialog.ShowDialog() = System.Windows.Forms.DialogResult.OK Then lokalizacjaPlikuGraficznego = open_dialog.FileName Dim bmp As New Bitmap(lokalizacjaPlikuGraficznego) Console.WriteLine("Wprowadź wartość przesunięcia?") Dim przesuniecie As Long = 0 Do Dim test As String = Console.ReadLine() If IsNumeric(test) Then przesuniecie = test Exit Do Else Console.WriteLine("Wprowadzona wartość nie jest liczbą.") End If Loop Dim niepoprawnie As Boolean = True Dim R As Integer = 0, G As Integer = 0, B As Integer = 0 Dim xmax As Integer = bmp.Width - 1 Dim ymax As Integer = bmp.Height - 1 Dim pixelElementIndex As Long = 0 'służy do określenia ile procent obrazu zostało zaszyfrowane Dim calkowitaIloscPx As Integer = bmp.Width * bmp.Height Dim aktualnaWartosc As Integer = 0 For y = 0 To ymax For x = 0 To xmax With bmp.GetPixel(x, y) For i As Integer = 0 To 255 If (((i * przesuniecie) - .R) Mod 256) = 0 Then R = i Exit For End If Next For i As Integer = 0 To 255 If (((i * przesuniecie) - .G) Mod 256) = 0 Then G = i Exit For End If Next For i As Integer = 0 To 255 If (((i * przesuniecie) - .B) Mod 256) = 0 Then B = i Exit For End If Next End With bmp.SetPixel(x, y, Color.FromArgb(R, G, B)) 'prezentuje procent postępu aktualnaWartosc += 1 Console.SetCursorPosition(0, Console.CursorTop) Console.Write((((aktualnaWartosc / calkowitaIloscPx) * 100)).ToString("00.00") & " %") Next x Next y Console.WriteLine() bmp.Save("C:\Users\piotr\Desktop\" + IO.Path.GetFileNameWithoutExtension(lokalizacjaPlikuGraficznego).ToString _ + "odszy.bmp", System.Drawing.Imaging.ImageFormat.Bmp) Console.WriteLine("Bity zostały odszyfrowane!") Console.ReadLine() End If End Sub End Module |
Oba te algorytmy działają na opisanej powyżej zasadzie. Przestawienie tekstu też nie powinno stanowić problemu:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
Imports System.Windows.Forms Module Module1 Dim wiadomoscZaszyfrowana As String = "" Sub Main() Dim open_dialog As New OpenFileDialog() open_dialog.InitialDirectory = "c:\" open_dialog.Filter = "Image Files (*.txt)|*.txt" If open_dialog.ShowDialog() = System.Windows.Forms.DialogResult.OK Then Dim tekstZpliku As String = IO.File.ReadAllText(open_dialog.FileName) Console.WriteLine("Wprowadź wartość przesunięcia dla szyfru podstawieniowego") Dim przesuniecie As Long = 0 'Czeka aż użytkownik wpisze liczbę pierwszą Do Dim test As String = Console.ReadLine() If IsNumeric(test) Then Dim twojaLiczbaJestPierwsza As Boolean = True ''algorytm sprawdza czy wpisana liczba jest pierwsza (wolna metoda) For i As Integer = 2 To Math.Ceiling(test / 2) If test Mod i = 0 Then twojaLiczbaJestPierwsza = False Exit For End If Next If twojaLiczbaJestPierwsza = True Then przesuniecie = test Exit Do Else Console.WriteLine("Twoja liczba nie jest liczbą pierwszą.") End If Else Console.WriteLine("Wprowadzona wartość nie jest liczbą.") End If Loop For i As Int32 = 0 To tekstZpliku.Length - 1 Dim k As Integer = Asc(tekstZpliku(i)) wiadomoscZaszyfrowana += Chr((k * przesuniecie) Mod 256) Next Console.Write("Podaj nazwę pliku pod którym chcesz zapisać plik txt: ") Dim nazwapliku As String = Console.ReadLine() IO.File.WriteAllText("C:\Users\piotr\Desktop\" + nazwapliku + ".txt", wiadomoscZaszyfrowana) Console.WriteLine("Bajty zostały ukryte. Zapisano plik: " + "C:\Users\piotr\Desktop\" + nazwapliku + ".txt") Console.ReadLine() End If End Sub End Module |
Mimo wszystko metoda ta nadal będzie podatna na analizę statystyczną, poprzez podstawianie pod znaki w kryptogramie litery najczęściej występujące dobierzemy dla każdej odpowiednie przesunięcie, można również zastosować metodą siłową (sprawdzając liczby pierwsze, których jest ograniczona ilość). Wszystkie te metody powinny przynieść skutek w miarę rozsądnym czasie, jeśli będziemy dysponowali odpowiednią ilością próbek. Model taki komplikuje fakt, że do utworzenia kryptogramu posłużyły trzy zmienne, których deszyfrant nie zna, nawet gdyby znał elementy ukryte to i tak trudno byłoby mu oszacować wartość, jaka została użyta do zaszyfrowania wiadomości, ponieważ:
Gdzie a,b,c jest zbiorem liczb naturalnych. Jedynie znając część obrazu jawnego, dalibyśmy radę odszyfrować obrazek poprzez określenie podstawień jej wartości względem wartości oryginalnej. Metodę tą można użyć również do szyfrowania struktury plików. Stworzenie bardziej złożonego modelu sprawia, że jego złamanie jest bardzo trudne.
Kod łączący liczby pierwsze i szyfr z kluczem:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 |
Imports System.Windows.Forms Imports System.Drawing Module Module1 Dim lokalizacjaPlikuGraficznego As String Sub Main() Dim open_dialog As New OpenFileDialog() open_dialog.InitialDirectory = "c:\" open_dialog.Title = "Wskaż plik który chcesz zaszyfrować." open_dialog.Filter = "Image Files (*.jpeg; *.png; *.bmp)|*.jpg; *.png; *.bmp" If open_dialog.ShowDialog() = System.Windows.Forms.DialogResult.OK Then lokalizacjaPlikuGraficznego = open_dialog.FileName Dim bmp As New Bitmap(lokalizacjaPlikuGraficznego) Console.Write("Zamierzasz zaszyfrować plik. Wprowadź klucz szyfrujący: ") Dim klucz As String = Console.ReadLine() 'dzieli klucz na wartości liczbowe z tabeli IOS Dim mojklucz(klucz.Length - 1) As Integer For i As Int32 = 0 To klucz.Length - 1 Dim s As Integer = Asc(klucz(i)) mojklucz(i) = s Next Dim przesuniecie As Integer = 139 'liczba pierwsza Dim R As Long = 0, G As Long = 0, B As Long = 0 Dim xmax As Integer = bmp.Width - 1 Dim ymax As Integer = bmp.Height - 1 Dim pixelElementIndex As Long = 0 'służy do określenia ile procent obrazu zostało zaszyfrowane Dim calkowitaIloscPx As Integer = bmp.Width * bmp.Height Dim aktualnaWartosc As Integer = 0 Dim k As Integer = 0 For y = 0 To ymax For x = 0 To xmax With bmp.GetPixel(x, y) 'podstawia wartości pod piksele R = (((.R * przesuniecie) Mod 256) + mojklucz(k Mod mojklucz.Length)) Mod 256 k += 1 G = (((.G * przesuniecie) Mod 256) + mojklucz(k Mod mojklucz.Length)) Mod 256 k += 1 B = (((.B * przesuniecie) Mod 256) + mojklucz(k Mod mojklucz.Length)) Mod 256 k += 1 End With 'zapisuje piksel bmp.SetPixel(x, y, Color.FromArgb(R, G, B)) 'prezentuje procent postępu aktualnaWartosc += 1 Console.SetCursorPosition(0, Console.CursorTop) Console.Write((((aktualnaWartosc / calkowitaIloscPx) * 100)).ToString("00.00") & " %") Next x Next y Console.WriteLine() 'zapisuje obrazek bmp.Save("C:\Users\piotr\Desktop\" + IO.Path.GetFileNameWithoutExtension(lokalizacjaPlikuGraficznego).ToString + ".bmp", System.Drawing.Imaging.ImageFormat.Bmp) Console.WriteLine("Bity zostały zaszyfrowane!") Console.ReadLine() End If End Sub End Module |
Kod deszyfrujący powyższą metodę
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 |
Imports System.Windows.Forms Imports System.Drawing Module Module1 Dim lokalizacjaPlikuGraficznego As String Sub Main() Dim open_dialog As New OpenFileDialog() open_dialog.InitialDirectory = "c:\" open_dialog.Title = "Wskaż zaszyfrowany plik." open_dialog.Filter = "Image Files (*.jpeg; *.png; *.bmp)|*.jpg; *.png; *.bmp" If open_dialog.ShowDialog() = System.Windows.Forms.DialogResult.OK Then lokalizacjaPlikuGraficznego = open_dialog.FileName Dim bmp As New Bitmap(lokalizacjaPlikuGraficznego) Console.Write("Wprowadź klucz szyfrujący: ") Dim klucz As String = Console.ReadLine() Dim przesuniecie As Integer = 139 ' liczba pierwsza 'dzieli klucz na wartości liczbowe z tabeli IOS Dim mojklucz(klucz.Length - 1) As Integer For i As Int32 = 0 To klucz.Length - 1 Dim s As Integer = Asc(klucz(i)) mojklucz(i) = s Next Dim niepoprawnie As Boolean = True Dim R As Integer = 0, G As Integer = 0, B As Integer = 0 Dim xmax As Integer = bmp.Width - 1 Dim ymax As Integer = bmp.Height - 1 Dim pixelElementIndex As Long = 0 'służy do określenia ile procent obrazu zostało zaszyfrowane Dim calkowitaIloscPx As Integer = bmp.Width * bmp.Height Dim aktualnaWartosc As Integer = 0 Dim k As Integer = 0 For y = 0 To ymax For x = 0 To xmax With bmp.GetPixel(x, y) R = (.R - mojklucz(k Mod mojklucz.Length)) If R < 0 Then R = 256 + R End If k += 1 For i As Integer = 0 To 255 If (((i * przesuniecie) - R) Mod 256) = 0 Then R = i Exit For End If Next G = (.G - mojklucz(k Mod mojklucz.Length)) If G < 0 Then G = 256 + G End If k += 1 For i As Integer = 0 To 255 If (((i * przesuniecie) - G) Mod 256) = 0 Then G = i Exit For End If Next B = (.B - mojklucz(k Mod mojklucz.Length)) If B < 0 Then B = 256 + CInt(B) End If k += 1 For i As Integer = 0 To 255 If (((i * przesuniecie) - B) Mod 256) = 0 Then B = i Exit For End If Next End With bmp.SetPixel(x, y, Color.FromArgb(R, G, B)) 'prezentuje procent postępu aktualnaWartosc += 1 Console.SetCursorPosition(0, Console.CursorTop) Console.Write((((aktualnaWartosc / calkowitaIloscPx) * 100)).ToString("00.00") & " %") Next x Next y Console.WriteLine() bmp.Save("C:\Users\piotr\Desktop\" + IO.Path.GetFileNameWithoutExtension(lokalizacjaPlikuGraficznego).ToString _ + "odszy.bmp", System.Drawing.Imaging.ImageFormat.Bmp) Console.WriteLine("Bity zostały odszyfrowane!") Console.ReadLine() End If End Sub End Module |
