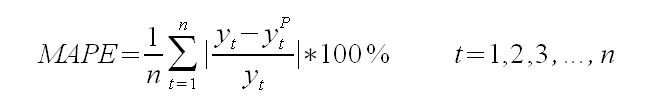Podstawową miarą pomiaru błędu między miarą prognozowaną a prognozą jest, błąd oznaczany jako E (error). Jest to różnica/odchylenie między zmienną prognozowaną a jej prognozą.
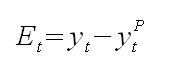 Jest to podstawowa miara błędu dla okresu ,,t”. Może ona być przedstawiona w formie procentowej. PE (percentage error) określa ona jaki procent zmiennej prognozowanej wynosi błąd prognozy.
Jest to podstawowa miara błędu dla okresu ,,t”. Może ona być przedstawiona w formie procentowej. PE (percentage error) określa ona jaki procent zmiennej prognozowanej wynosi błąd prognozy.
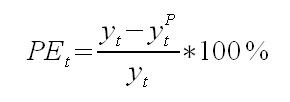 Są to miary odwołujące się do pojedynczych obserwacji. Aby określić błąd dla całej metody lub modelu, który wykorzystujemy, stosujemy miarę zwaną średnim błędem ME (mean error). Określamy ją wzorem:
Są to miary odwołujące się do pojedynczych obserwacji. Aby określić błąd dla całej metody lub modelu, który wykorzystujemy, stosujemy miarę zwaną średnim błędem ME (mean error). Określamy ją wzorem:
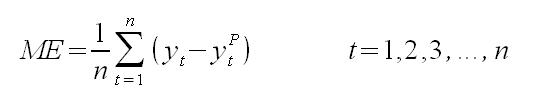 Dla metody idealnej wartość ta powinna być równa zero lub bardzo niska. Logiczne jest, że podczas tworzenia modelu i jego dopasowaniu, idealny model będzie miał prognozy wygasłe w jak najmniejszym stopniu różniące się od danych prognozowanych, a ostatecznie ich średnia będzie jak najmniejsza. Na podstawie znaku miernika ME można sądzić, że gdy znak jego jest dodatni, nasze prognozy wygasłe są nieoszacowane, a gdy znak miernika jest ujemny, nasze prognozy wygasłe są przeszacowane. Oczywiście żaden model ani metoda nie da nam ME równego zeru, gdyż każda metoda i model jest obciążona błędem, nawet bardzo niskim w modelu zazwyczaj dążymy do osiągnięcia ME jak najmniejszego. Odmianą tego miernika jest średni procentowy błąd MPE (mean percentage error), który definiujemy wzorem:
Dla metody idealnej wartość ta powinna być równa zero lub bardzo niska. Logiczne jest, że podczas tworzenia modelu i jego dopasowaniu, idealny model będzie miał prognozy wygasłe w jak najmniejszym stopniu różniące się od danych prognozowanych, a ostatecznie ich średnia będzie jak najmniejsza. Na podstawie znaku miernika ME można sądzić, że gdy znak jego jest dodatni, nasze prognozy wygasłe są nieoszacowane, a gdy znak miernika jest ujemny, nasze prognozy wygasłe są przeszacowane. Oczywiście żaden model ani metoda nie da nam ME równego zeru, gdyż każda metoda i model jest obciążona błędem, nawet bardzo niskim w modelu zazwyczaj dążymy do osiągnięcia ME jak najmniejszego. Odmianą tego miernika jest średni procentowy błąd MPE (mean percentage error), który definiujemy wzorem:
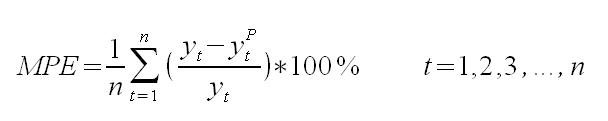 Kolejną miarą jest średni błąd bezwzględny MAE (mean absolute error), informuje on o ile średnio w okresie prognoz, będzie wynosić odchylenie od wartości rzeczywistej. Czyli, krótko mówiąc, o jakim błędem miarowym jest obarczona nasza prognoza.
Kolejną miarą jest średni błąd bezwzględny MAE (mean absolute error), informuje on o ile średnio w okresie prognoz, będzie wynosić odchylenie od wartości rzeczywistej. Czyli, krótko mówiąc, o jakim błędem miarowym jest obarczona nasza prognoza.
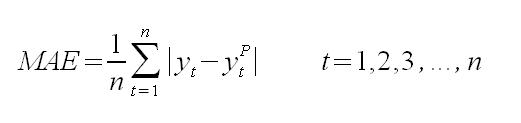 Czyli jeśli za pomocą jakiegoś modelu otrzymamy prognozę równą „44” a po obliczeniu MAE dla okresu testowego wyniesie ono Mae = 2,456, wtedy nasza prognoza = 44 może odbiegać od rzeczywistej wartości przyszłej o 2,456 czyli może być z przedziału od 41,544 do 46,456.
Czyli jeśli za pomocą jakiegoś modelu otrzymamy prognozę równą „44” a po obliczeniu MAE dla okresu testowego wyniesie ono Mae = 2,456, wtedy nasza prognoza = 44 może odbiegać od rzeczywistej wartości przyszłej o 2,456 czyli może być z przedziału od 41,544 do 46,456.
Następną miarą, jaką się zajmiemy, jest bliźniacza miara MAE. Średni bezwzględny błąd procentowy MAPE (mean absolute percentage error) informuje on o średniej wielkości błędów prognoz dla okresu testowego, wyrażonych w procentach. Wartość MAPE pozwala na porównanie dokładność prognoz różnych modeli.
lub dla porównania prognozy:
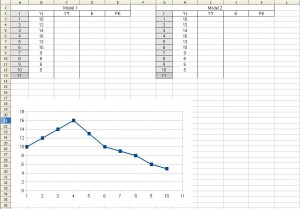
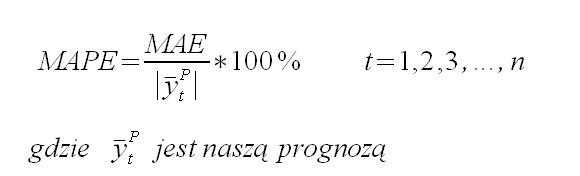 Jak wygląda to w praktyce, zademonstruje na przykładzie pliku Excel, Powiedzmy, że mam jakieś dane, na których będę pracował i wykorzystuje dwa modele prognostyczne (ja użyłem metody Browna jedna dla modelu z alfa =0,4 a drugi z alfa=0,7):
Jak wygląda to w praktyce, zademonstruje na przykładzie pliku Excel, Powiedzmy, że mam jakieś dane, na których będę pracował i wykorzystuje dwa modele prognostyczne (ja użyłem metody Browna jedna dla modelu z alfa =0,4 a drugi z alfa=0,7):
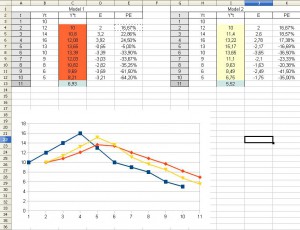
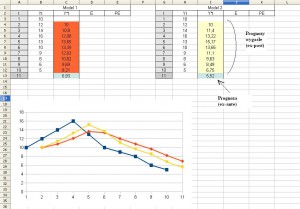
 Po użyciu moich modeli dostałem następujące wartości
Po użyciu moich modeli dostałem następujące wartości
 Wypełniamy Nasze błędy E i PE dla prognoz wygasłych:
Wypełniamy Nasze błędy E i PE dla prognoz wygasłych:
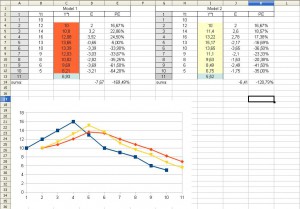 Na podstawie wzorów powyżej obliczamy ME, MPE:
Na podstawie wzorów powyżej obliczamy ME, MPE:
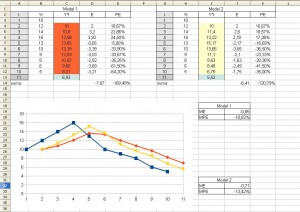 Zostały nam do obliczenia MAE i MAPE, aby tego dokonać dodamy sobie dodatkowe kolumny i obliczymy ich sumy:
Zostały nam do obliczenia MAE i MAPE, aby tego dokonać dodamy sobie dodatkowe kolumny i obliczymy ich sumy:
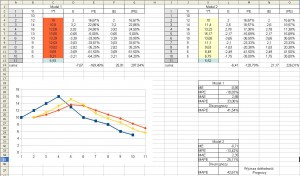
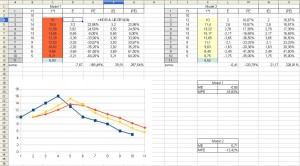 Po obliczeniu wartości wyniosą:
Po obliczeniu wartości wyniosą:
Jak widzimy prognoza w drugim modelu ma wyższy współczynnik czyli jest bardziej prawdopodobna niż prognoza w modelu pierwszym ponadto reszta współczynników w modelu drugim jest mniejsza co świadczy o wyższym współczynniku prawdopodobieństwa dla modelu drugiego.
Plik excel można pobrać tutaj: Błąd E, błąd procentowy EP, średni błąd ME, średni procentowy błąd MPE, średni błąd bezwzględny MAE, średni bezwzględny błąd procentowy MAPE
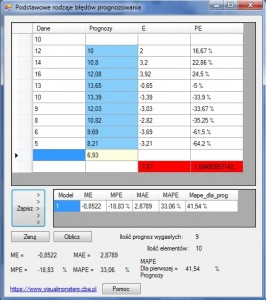
Zapraszam również do pobrania programu który ułatwi wam obliczanie podstawowych rodzajów błędów,
Można go pobrać tutaj: E_PE_ME_MPE_MAE_MAPE