Kurtoza

Kurtoza to miara koncentracji uzyskanych wyników. Określa jak wiele naszych wyników jest zbliżona do wartości średniej oraz czy większość z uzyskanych wyników ma wartość podobną do średniej. Jeżeli kurtoza jest niska (poniżej zera) to w zbiorze danych możemy zaobserwować większą liczbę wyników znacznie oddalonych od średniej, gdy kurtoza jest wyższa tym liczba takich obserwacji maleje. 

Interpretacja kurtozy

Rozkłady prawdopodobieństwa można podzielić ze względu na wartość kurtozy na rozkłady:

• Ku=3 (i Ex=0) – rozkład mezokurtyczny – spłaszczenie rozkładu jest podobne do spłaszczenia rozkładu normalnego (dla którego kurtoza wynosi dokładnie 0).
• Ku>3 (i Ex>0) – rozkład leptokurtyczny – wartości cechy bardziej skoncentrowane (bardziej wysmukłe) niż przy rozkładzie normalnym.
• Ku<3 (i Ex<0) – rozkład platokurtyczny – kurtoza jest ujemna, wartości cechy mniej skoncentrowane (bardziej spłaszczone) niż przy rozkładzie normalnym.

Przykład:

W klasie 26 uczniów ze sprawdzianu dzieci dostały następujące oceny:

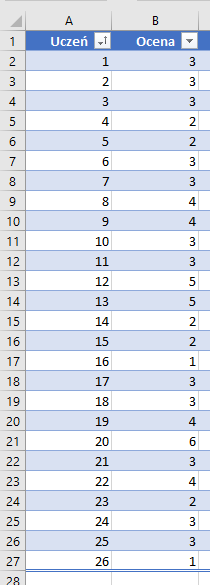
Aby obliczyć Kurtozę, potrzebujemy dwuch elementów

• Czwarty moment centralny
• Odchylenie standardowe

Zaczniemy od czwartego momentu centralnego, obliczymy go wzorem :

=Table1[[#Totals],[(xi-avg)^4]]/A27

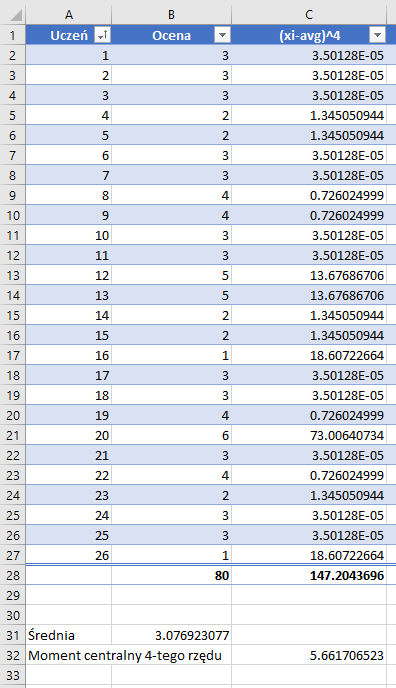
Odchylenie standardowe obliczymy wzorem:

=SQRT(Table1[[#Totals],[(xi-avg)^2]]/(A27-1))

lub

=STDEV.S(Table1[Ocena])

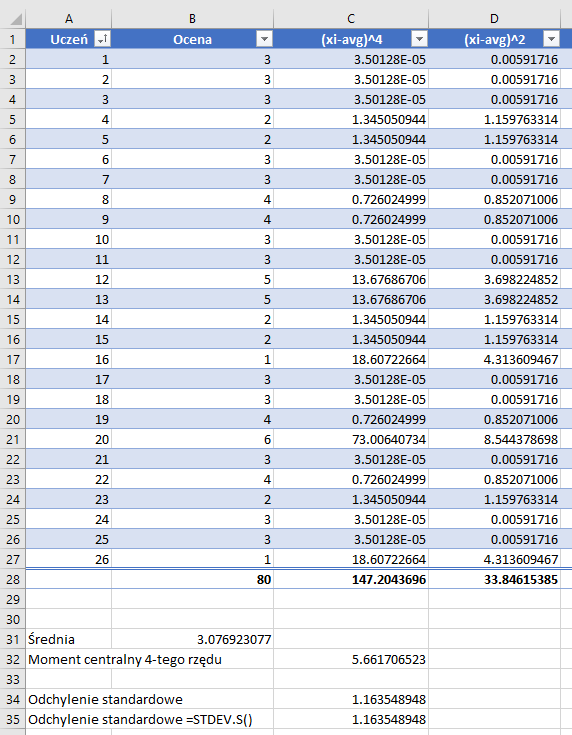
Po uzyskaniu zmiennych, jesteśmy w stanie obliczyć Kurtoze:

=KURT(Table1[Ocena])

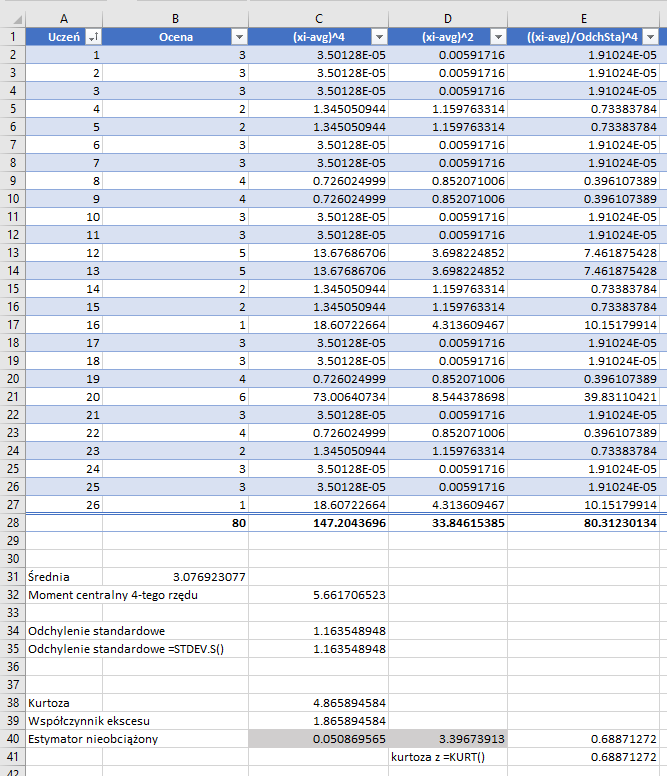
Powyżej mamy przykład obliczeń kurtozy na kilka sposobów, Excel do swoich obliczeń wykorzystuje estymator nieobciążony.

Plik excel do pobrania: