Model ten jest dużo lepszy od modelu Browna. Wykorzystujemy w nim dwa parametry wygładzania: alfa i beta. Jest to bardzo ciekawa metoda. Można ją dostosować do do dalszych prognoz sięgających w przód. Nadaje się również do wygładzania. Metoda wykorzystywana głównie gdy w szeregu występują małe wahania przypadkowe i trend liniowy lecz nie ma w nim sezonowości. Wygładzanie obejmuje zarówno poziom zmiennej jak i jej przyrost. Program do obliczania tego modelu można pobrac tutaj: Model Liniowy Holta wersja 1.2
Program działa dla komputerów z systemem operacyjnym Windows 7+
Tak jak pisałem wcześniej w modelu wykorzystujemy dwa parametry wygładzania
-Ft- Szacuje wahania przypadkowe
-St – Szacuje trend
Prognozę wygasłą obliczamy za pomocą wzoru:
Samą prognozę wyznaczamy wzorem:
Tak jak zaznaczałem na początku program który stworzymy będzie wyznaczał prognozę tylko dla T=1. Nie stoi nic na przeszkodzie aby ten element rozwinąć. Osobom trochę wprawionym dodanie takiej opcji nie powinno sprawić trudności.
Za wartość początkową F1 zazwyczaj przyjmujemy y1. Wartość początkową S1 przyjmujemy na dwa sposoby
1. S1=0
2. S1 = y2-y1
Pokażę teraz jak to obliczyć w excelu. Dodajemy dane do arkusza, ja mam 40 obserwacji:
Teraz należy podjąć decyzję o wyborze pierwszych współczynników, tak jak pisałem na początku popularne metody to albo y1 dla F1 i 0 dla S1 lub średnia z dwóch pierwszych obserwacji. Ja wybieram y1 dla F1 i S1 = y2-y1
Określamy sobie teraz początkowe wartości dla alfy i bety u mnie będzie to a=0.4, b=0,4 nie martwcie się później doszlifujemy to solverem potrzebujemy ich tylko na początku.
Obliczamy Ft i St równocześnie
Obliczamy prognozę według wzoru i istotne elementy do sprawdzenia dopasowania prognoz i błędu
Dodajemy kluczowe elementy oceny błędu, ME, MSE, RMSE
Zajmiemy się teraz prognozami. Chcemy dodać sobie jeszcze ze dwie prognozy i ocenić jej dopuszczalność ( jaki jej procent będzie błędny). Pierwsza prognoza to nie problem, robi się z automatu.
Ocenę dopuszczalności dla ostatniej prognozy i środkowej obliczamy w taki sam sposób jak pierwszą wartość ale dodajemy poprzednie wartości ponieważ jeśli dla pierwszej prognozy błąd wynosi 2,8% to dla drugiej będzie wynosił (jej błąd %) + 2,8%. Aby określić najlepsze współczynniki dla alfy i bety użyjemy solvera tak samo jak było to w przypadku Modelu Browna tylko dla dwóch wartości.
Po jego uruchomieniu program będzie szukał wartości
Ostatecznie RMSE otrzymuje najmniejszą wartość gdy:
Kiedy użyjemy programu do obliczeń tego modelu, dostępnego do pobrania na tej stronie otrzymamy zbliżoną wartość:
Plik excel z całą procedurą dostępny tutaj: Holt_model
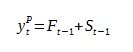






2 komentarze
Witam, możliwe jest że w momencie przeliczenia RMSE przez solvera wychodzi beta na 0 ?
Mój wynik:
Współczynnik
Komórka Nazwa wartość
$K$4 RMSE = 1,612087282
Zmienna
Komórka Nazwa wartość
$I$2 α 0,783505769
$I$3 β 0
$I$4 γ 1
Autor
Witaj,
całkiem możliwe, spróbuj wrócić dane tutaj do tego programu
https://visualmonsters.cba.pl/index.php/prognozowanie/pomoc-i-obsluga-programu-model-liniowy-holta/
https://visualmonsters.cba.pl/index.php/model-multiplikatywnyaddytywny-wintersa2/
i zobaczyć wykresy, jeśli najmniejsze RMSE otrzymasz dla takiej kombinacji, znaczy to, że twoje dane mogą nie zawierać jakiegoś czynnika, gdyż każda ze zmiennych odpowiada za:
* Poziom zmiennej, reprezentowany przez parametr α (alfa) wygładza wahania przypadkowe, α∈<0,1>
* Przyrost, reprezentowany przez parametr β (beta) wygładza trend, β∈<0,1>
* Sezonowość, reprezentowany przez parametr γ (gamma) wygładza trend, γ ∈<0,1>
Trzeba mieć na uwadzę, że Solver to tylko maszyna, wybierze to, co jest dla niego najodpowiedniejsze.