Jest to jedna z najprostszych metod prognozowania. Polega na wygładzeniu zmiennych poprzez ich średnią, kiedy w naszych danych występuje duży błąd losowy, najprostszą metodą jego wyeliminowania jest właśnie średnia ruchoma. Średnia ruchoma działa jak filtr, eliminując z szeregu wahania krótkookresowe. Metodę tą wykorzystujemy w szeregach bez trendu i sezonowości za to z dowolnymi wahaniami przypadkowymi. Jej obliczanie jest bardzo proste dlatego często wykorzystywana na różnych rodzajach wykresów giełdowych jako indykator, gdzie próżno szukać sezonowości i właśnie trendu. Zakłada ona, że wartość zmiennej w okresie prognozy będzie równa średniej arytmetycznej z jej „k” poprzednich wartości gdzie „k- stała wygładzania”, określana z góry na początku obliczeń. Prognoza dla takiego modelu zazwyczaj opatrzona jest dużym błędem, ale może posłużyć jako sugestia rozwojowa szeregu. Wyznaczamy ją wzorem:
Prognozy wyższe niż jeden okres ex-ante wykonujemy poprzez włączenie prognoz wykonanych na okresy wcześniejsze. Wraz ze wzrostem współczynnika „i” wzrasta efekt wygładzenia, ale zwiększa błąd prognozy i zmniejsza reakcję na zmiany poziomu prognozowanej zmiennej. Niski wskaźnik współczynnika sprawia za to, że na prognozę silniej wpływają wahania przypadkowe. Należy unikać wygładzenia zbyt silnego z powodu utraty pewnej części informacji, jest to spowodowane sposobem, w jaki szacujemy prognozy ex-post. Zróbmy przykład takiego wykorzystania średniej ruchomej w Excelu. Dodamy dane:
 Przedstawię tutaj kilka średnich ruchomych, pierwsza k=2 będzie oczywiście równa (50+35)/2. Po obliczeniu wygląda to tak:
Przedstawię tutaj kilka średnich ruchomych, pierwsza k=2 będzie oczywiście równa (50+35)/2. Po obliczeniu wygląda to tak:
 Przy wysokim k nasze dane są bardzo wygładzone, co widać na wykresie, panujący trend widać gołym okiem. Prognozy dodałem w następujący sposób:
Przy wysokim k nasze dane są bardzo wygładzone, co widać na wykresie, panujący trend widać gołym okiem. Prognozy dodałem w następujący sposób:
 Brakujące dane zastępujemy danymi otrzymanymi wskutek prognozy. Jak wygląda błąd takiego modelu:
Brakujące dane zastępujemy danymi otrzymanymi wskutek prognozy. Jak wygląda błąd takiego modelu:
 Jak widzimy powyżej z oceny dopuszczalności, w każdej z prognoz występuje dość duży odsetek błędu. Dla danych powyższych ocena jakości modelu prognostycznego nie napawa optymizmem, sugerowanie się takimi prognozami może oznaczać duże ryzyko. Postaramy się zmniejszyć powyższy błąd przy użyciu Solvera i metody średniej ważonej. Zwróć uwagę, w jaki sposób wzrost współczynnika „k” wpływa na efekt wygładzenia, przy dużym współczynniku, wygładzeniu ulegają nawet duże wahania przypadkowe. Z reguły jest tak, że bieżące dane mają większy wpływ na kształtowanie się szeregu niż dane w bardziej odległej przeszłości. Na tej zasadzie bazuje metoda średniej ruchomej ważonej, którą przedstawiamy wzorem:
Jak widzimy powyżej z oceny dopuszczalności, w każdej z prognoz występuje dość duży odsetek błędu. Dla danych powyższych ocena jakości modelu prognostycznego nie napawa optymizmem, sugerowanie się takimi prognozami może oznaczać duże ryzyko. Postaramy się zmniejszyć powyższy błąd przy użyciu Solvera i metody średniej ważonej. Zwróć uwagę, w jaki sposób wzrost współczynnika „k” wpływa na efekt wygładzenia, przy dużym współczynniku, wygładzeniu ulegają nawet duże wahania przypadkowe. Z reguły jest tak, że bieżące dane mają większy wpływ na kształtowanie się szeregu niż dane w bardziej odległej przeszłości. Na tej zasadzie bazuje metoda średniej ruchomej ważonej, którą przedstawiamy wzorem:
Wracamy do naszego dokumentu. Dodajemy wagi tak jak na obrazku i chwilowo nie manipulujemy za bardzo przy ich wartościach.
Ja dodałem takie na oko. Należy jeszcze dodać komórkę sumującą nasze wagi. Odpalamy Solvera i używamy go tak jak na obrazku:
Komórka docelowa: (komórka RMSA)
Zoptymalizuj wynik pod kątem: Minimum
Poprzez zmianę komórki: (komórki zawierające zmienne w1 i w2)
Warunki ograniczeń:(w1>=0,w1<=1, w2>=0,w2<=1, suma w: =1)
Po obliczeniu przefiltrowaniu wszystkich modeli Solverem otrzymałem optymalne wagi:
Jak widzimy zadziwiająco dobrze dopasowany jest model dla k=4 gdyż wstrzeliliśmy się w jego sezon.
To, co zrobiliśmy to wygładzanie naszego szeregu. Jeśli pamiętasz, co pisałem na początku strony, aby móc prognozować, za pomocą średniej ruchomej nasz szereg w okresie diagnozy musi podlegać tylko wahaniom losowym, w innym wypadku, proces był niestacjonarny i musimy sprowadzić go do procesu stacjonarnego. Aby tego dokonać musimy pozbyć się trendu, wahań sezonowych i wahań cyklicznych, można to zrobić poprzez:
- Dekompozycje szeregu czasowego
- Przy pomocy różnicowania
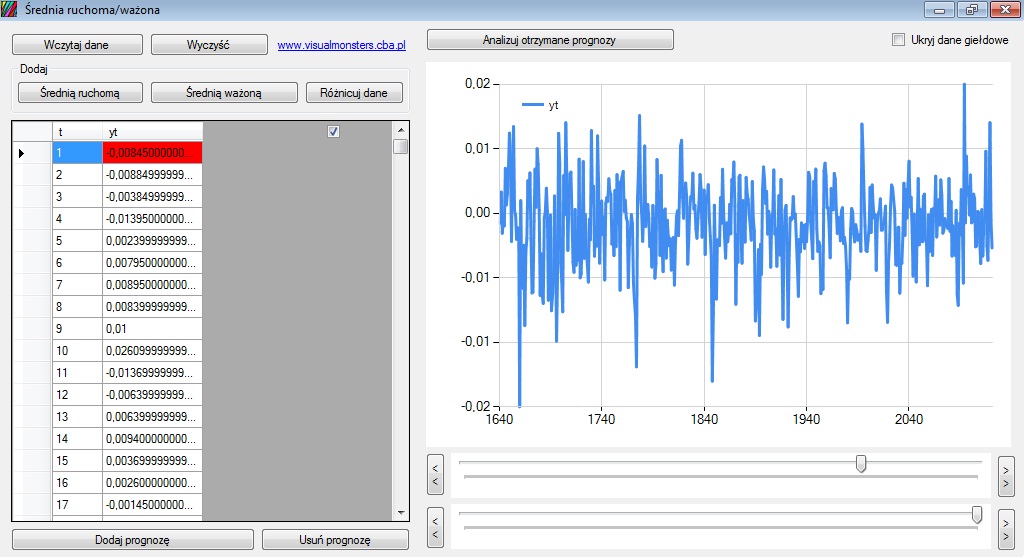
Najprostszą i najszybszą metodą jest różnicowanie. Jak różnicować dowiecie się ze strony na blogu „Różnicowanie szeregu” do którego lektury gorąco zachęcam. Wracając do tematu, mamy szereg czasowy (dane z MT4 USD/CHF). Bez różnicowania, używając analogicznej metody podanej powyżej nasz szereg nie będzie miał dalekiej prognozy:
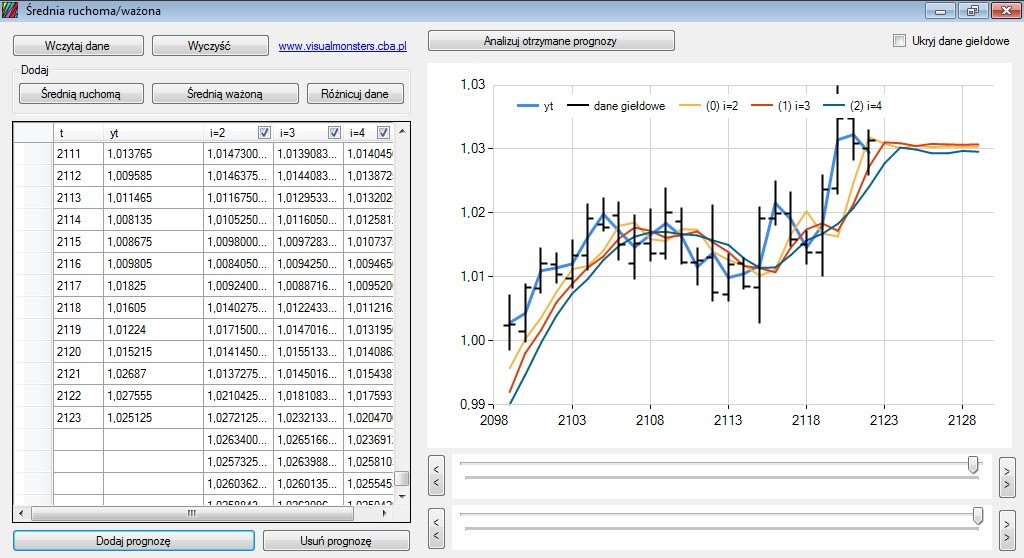
Ponadto, prognoza taka nie wzbudza zaufania i kompletnie nic na nie mówi o przyszłych losach naszego szeregu. Jednakże tak wygładzone dane można wykorzystać w celu uzyskania bardziej efektywnych prognoz dla innych modelów jak na przykład autoregresja. Jednakże, jeśli zróżnicujemy dane, efekt będzie dużo lepszy:
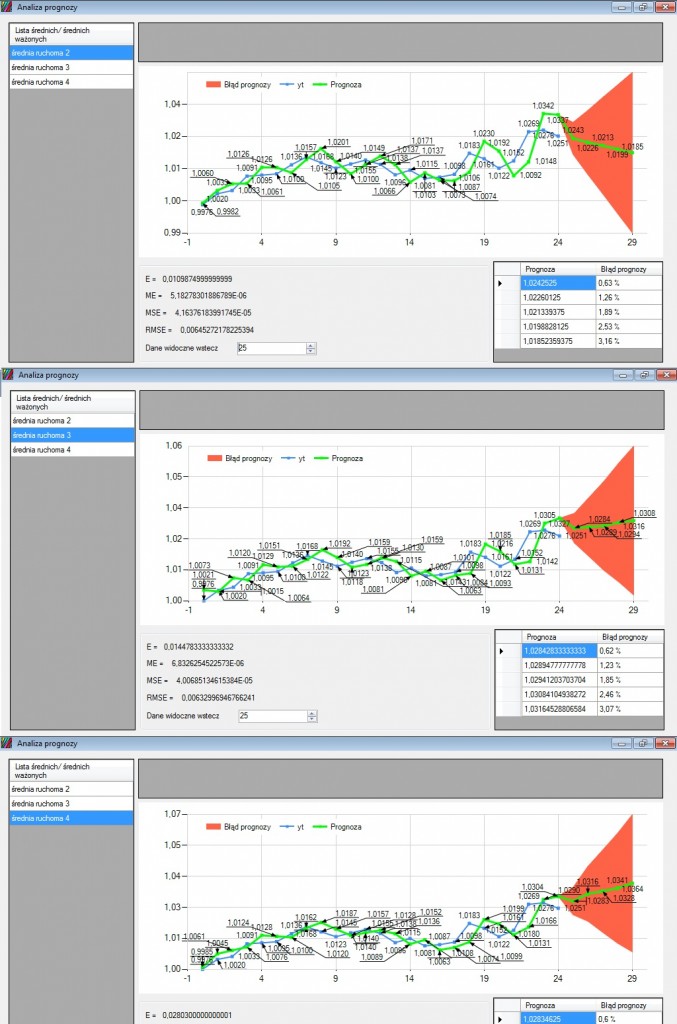
Tak zróżnicowany szereg można nazwać stacjonarnym a prognozy dla MA(2,1), MA(3,1), MA(4,1) wyglądają tak:
Taka prognoza informuje nas o dalszym przebiegu trendu (w tym wypadku oczekujemy trendu zwyżkowego) i jest lepiej dopasowana. Dużo lepsze efekty dopasowania uzyskamy również łącząc różnicowanie i średnią ważoną.
Plik Excel dostępny tutaj: srednie.xls
Plik ODS dostępny tutaj: srednie.ods