Model Browna to jeden z prostych modeli prognostycznych. Zwykle stosuje się ten model dla szeregów czasowych o stałym poziomie lub bardzo słabym trendzie i umiarkowanych wahaniach przypadkowych. Jest on rozwinięciem modelu średnich ważonych.
Prognozę ex-ante i ex-post wyznaczamy na podstawie wzoru:
Pierwszy wyraz naszej prognozy
zazwyczaj przyjmujemy wartość:
1. Pierwszą wartość szeregu czasowego ( ten rodzaj określenia pierwszego wyrazu prognozy został wykorzystany w programie)
2. Średnią z trzech początkowych wartości szeregu czasowego.
3. Średnią z pięciu początkowych wyrazów szeregu czasowego.
Model ten w wielu przypadkach jest mało użyteczny, zazwyczaj dane ex-post wykazują słabe dopasowanie modelu do danych. Zazwyczaj współczynnik α osiąga najmniejsze wartości dla 1, należy wtedy przyjąć wartość α z przedziału <0.3,0.4> i potraktować model jako wygładzanie szeregu lub potraktować go jako informacje o panującym trendzie. Aby przybliżyć wam funkcjonowanie tego modelu posłużę się programem do wyliczania modelu Browna dostępnego tutaj : Model Wygladzania Wykladniczego Browna wersja 1.3b
i danymi dostępnymi tutaj: Model Browna
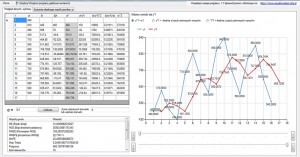
Po wprowadzeniu danych do programu wartość α ustawiana jest domyślnie na poziomie 0,4.
Jak widzimy model powstały przy użyciu wartości α na poziomie 0,4 jest dosyć słabo dopasowany do naszej zmiennej. Średni błąd RMSE wynosi 159,26… musimy go zmniejszyć do minimalnej wartości w tym celu możemy zmienić rodzaj powstawania pierwszych elementów prognozy ex-post w domyślnych opcjach wartość pierwszego współczynnika y*1 równy jest pierwszej wartości ciągu, po zmianie tej zależności na „Średnią z pięciu początkowych wyrazów szeregu czasowego” nasz średni błąd RMSE spada i wynosi 156,20…
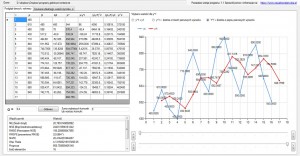
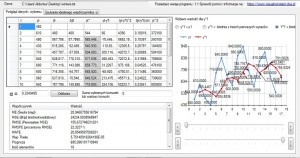
Należy teraz sprawdzić dla jakiej wartości α nasz model osiąga najlepsze dopasowanie.W tym celu przechodzimy na zakładkę „Szukanie idealnych współczynników α” Tam wybieramy wskaźnik który chcemy obniżyć do minimum domyślnie ustawiony jest wskaźnik RMSE, moim zdaniem jego mniejsza wartość ma największy wpływ na najlepsze dopasowanie modelu. Po wciśnięciu przycisku „Szukaj” program za pomocą szybkiego algorytmu poszuka najmniejszej wartości α do 7 liczb po przecinku.
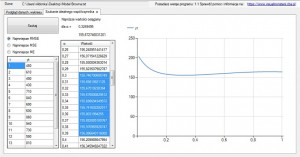Po prawej stronie widzimy, że nasz wykres wyraźnie ma wybrzuszenie które zawiera najniższe wartości RMSE dla α z przedziału (0,1). Wykres ten przedstawia rzutowanie wartości RMSE na wartości α,niektóre z tych danych przestawione są w generowanych po lewej stronie kolumnach, na podstawie tych kolumn tworzony jest wykres. Najmniejszy współczynnik α zostanie natychmiast zaimportowany i obliczony.
Jak widzimy po zmianie współczynnika wartość RMSE zmieniła się nieznacznie. Model taki można potraktować jako wygładzenie, zapowiedź trendu lub jego podtrzymanie. Pracując z tym modelem, sami musicie określić jego przydatność i odkryć sekrety. Przykład użycia tego modelu w excelu jest bardzo prosty. Dodajemy dane do arkusza:
Teraz mamy trzy możliwości wyboru pierwszego wyrażenia albo przyjmiemy, że pierwszym wyrazem będzie 480 lub średnia z trzech pierwszych wyrazów ciągu lub średnia z pięciu pierwszych wyrazów ciągu. Jest to zabieg opcjonalny który nie ma większego wpływu gdy nasz ciąg zawiera dużo danych. Ja wybiorę pierwszy wyraz z ciągu, określamy sobie na początek jakiś współczynnik alfa, może być 0,4 i obliczamy pierwszy współczynnik:
Wzór na ten współczynnik to ^yt =C3*$K$2+(1-$K$2)*B3 => (^yt * α ) + (1- α ) * yt
Δyt = C3-C2 => ( Δyt – Δy(t-1))
y*t = $K$2*B3+(1-$K$2)*E3 => (yt * α ) + (1- α ) * y*t
Dodajemy resztę współczynników, aby obliczyć wartość bezwzględną należy użyć funkcji =MODUŁ.LICZBY( F3/B3)
Teraz potrzebujemy jakiegoś współczynnika dopasowania ja wybrałem 3 takie współczynniki
Dodajemy wykres
Wszystko gotowe ale teraz przejdziemy do konkretów. Jak wybrać wartość alfa aby nasza prognoza była jak najlepiej dopasowana, należy użyć Solvera aby znaleźć takie wartości współczynnika alfa które dadzą najmniejsze RMSE:
Otrzymałem wynik:
Pokrywa się to w pewien sposób z tym co wylicza program który przedstawiałem na początku tej strony:
Plik Excel z rozwiązaniem dostępny tutaj: Brown
