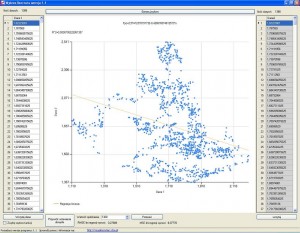
Wykres rozrzutu jest graficzną interpretacją korelacji. W wykresie takim jedna oś odpowiada wynikom dla jednej zmiennej, natomiast druga oś odpowiada wynikom drugiej zmiennej. Wykres taki odzwierciedla wzajemne relacje pomiędzy dwiema zmiennymi.
Za pomocą wykresów rozrzutu możemy stwierdzić z jakim rodzajem związku zmiennych X i Y mamy do czynienia. Poniżej przedstawiono zależność dodatnią wraz z linią regresji liniowej:
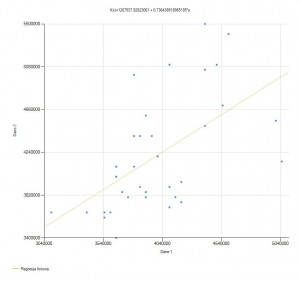 Z wykresu tego można wywnioskować, że wzrost wyników na jednej zmiennej towarzyszy wzrostowi wyników drugiej zmiennej.
Z wykresu tego można wywnioskować, że wzrost wyników na jednej zmiennej towarzyszy wzrostowi wyników drugiej zmiennej.
Drugi rodzaj zależności to zależność ujemna:
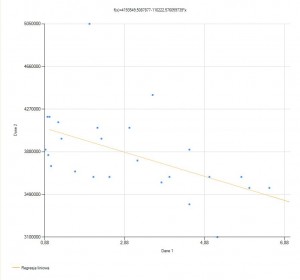 Analogicznie, ujemny związek oznacza, że wzrost wyników na jednej zmiennej towarzyszy spadkom wyników drugiej zmiennej.Istnieje możliwość, że zależności nie będzie albo będzie ona bardzo mała tak jak na wykresie :
Analogicznie, ujemny związek oznacza, że wzrost wyników na jednej zmiennej towarzyszy spadkom wyników drugiej zmiennej.Istnieje możliwość, że zależności nie będzie albo będzie ona bardzo mała tak jak na wykresie :
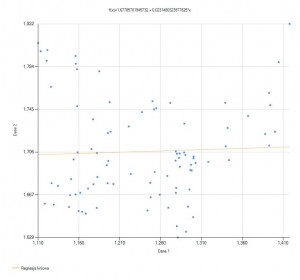 Wykresy rozrzutu mogą okazać się bardzo pomocne podczas prognozowania. Za ich pomocą i za pomocą linii regresji jesteśmy w stanie prognozować zjawiska zarówno ze zmiennymi zależnymi od innych zmiennych, czasu albo zależnymi od samych siebie (Autoregresja) pokażę te sposoby w excelu następnie zaprezentuje program który na pewno pomoże wam w prognozowaniu i interpretacji wykresów rozrzutu.
Wykresy rozrzutu mogą okazać się bardzo pomocne podczas prognozowania. Za ich pomocą i za pomocą linii regresji jesteśmy w stanie prognozować zjawiska zarówno ze zmiennymi zależnymi od innych zmiennych, czasu albo zależnymi od samych siebie (Autoregresja) pokażę te sposoby w excelu następnie zaprezentuje program który na pewno pomoże wam w prognozowaniu i interpretacji wykresów rozrzutu.
Prognozowanie zmiennych zależnych
Wstawiamy dwie zmienne do arkusza kalkulacyjnego:
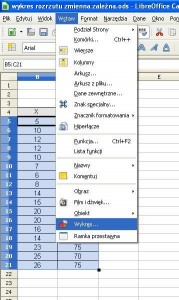
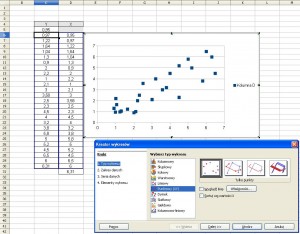
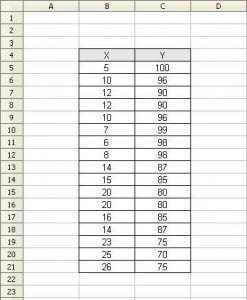 Następnie zaznaczamy obie kolumny, przechodzimy do zakładki „Wstaw” i wybieramy „Wykres”
Następnie zaznaczamy obie kolumny, przechodzimy do zakładki „Wstaw” i wybieramy „Wykres”
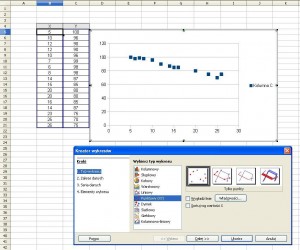 Wybieramy wykres „Punktowy (XY)”
Wybieramy wykres „Punktowy (XY)”
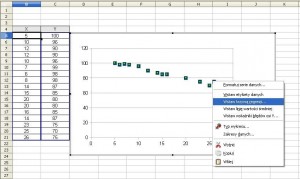
 Gdy pojawi się wykres rozrzutu klikamy dwa razy na wykres, następnie zaznaczamy naszą serie danych (klikając na nią dwukrotnie). Przyciskamy prawy klawisz myszy i wybieramy „Wstaw krzywą regresji …”
Gdy pojawi się wykres rozrzutu klikamy dwa razy na wykres, następnie zaznaczamy naszą serie danych (klikając na nią dwukrotnie). Przyciskamy prawy klawisz myszy i wybieramy „Wstaw krzywą regresji …”
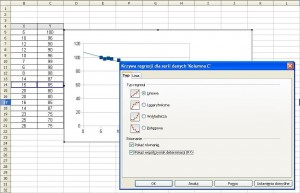
 W oknie edycji krzywej regresji wybieramy interesującą nas krzywą i zaznaczamy opcję „Pokaż równanie” i zaznaczamy opcje :
W oknie edycji krzywej regresji wybieramy interesującą nas krzywą i zaznaczamy opcję „Pokaż równanie” i zaznaczamy opcje :
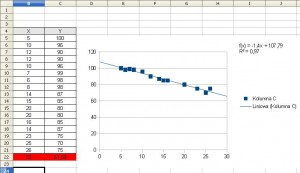
 Na wykresie powinien pokazać się wzór funkcji. Za pomocą tego wzoru możemy prognozować zjawiska. Jeśli pierwsza kolumna (Y) była temperaturą powietrza w danym dniu a druga kolumna (X) ilość osób odwiedzających sklep wtedy na podstawie prognozy pogody można określić ile osób odwiedzi nasz sklep. Z prognozy pogody wynika, że temperatura następnego dnia wyniesie 33 stopnie C. Prognoza dla takiej temperatury wyniesie: -1,4 * 33 + 107,79 = 61,59
Na wykresie powinien pokazać się wzór funkcji. Za pomocą tego wzoru możemy prognozować zjawiska. Jeśli pierwsza kolumna (Y) była temperaturą powietrza w danym dniu a druga kolumna (X) ilość osób odwiedzających sklep wtedy na podstawie prognozy pogody można określić ile osób odwiedzi nasz sklep. Z prognozy pogody wynika, że temperatura następnego dnia wyniesie 33 stopnie C. Prognoza dla takiej temperatury wyniesie: -1,4 * 33 + 107,79 = 61,59
 Do wykresu istnieje możliwość dołączenie współczynnika determinacji jest on jedną z podstawowych miar jakości dopasowania modelu. Przyjmuje on wartość od 0 do 1 i interpretuje się go w następujący sposób:
Do wykresu istnieje możliwość dołączenie współczynnika determinacji jest on jedną z podstawowych miar jakości dopasowania modelu. Przyjmuje on wartość od 0 do 1 i interpretuje się go w następujący sposób:
- 0,0 – 0,5 – dopasowanie niezadowalające
- 0,5 – 0,6 – dopasowanie słabe
- 0,6 – 0,8 – dopasowanie zadowalające
- 0,8 – 0,9 – dopasowanie dobre
- 0,9 – 1,0 – dopasowanie bardzo dobre
Wyjaśnia on w jakim stopniu model wyjaśnia kształtowanie się zmiennej objaśnianej. Wzór wygląda następująco:
 Nasz model ma wysoki współczynnik determinacji oznacza to, że bez problemów możemy za jego pomocą prognozować.
Nasz model ma wysoki współczynnik determinacji oznacza to, że bez problemów możemy za jego pomocą prognozować.
Arkusz kalkulacyjny można pobrać tutaj: wykres rozrzutu zmienna zależna
Prognozowanie szeregów czasowych
Prognozowanie szeregu czasowego wygląda podobnie z tą różnicą, że do dyspozycji będziemy mieli tylko jedną zmienną:
 Następnie zaznaczamy nasze dane i wstawiamy wykres.
Następnie zaznaczamy nasze dane i wstawiamy wykres.
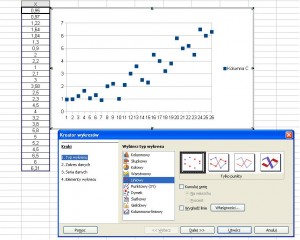 Wybieramy wykres punktowy i wstawiamy krzywą regresji tak jak to było opisane wcześniej.
Wybieramy wykres punktowy i wstawiamy krzywą regresji tak jak to było opisane wcześniej.
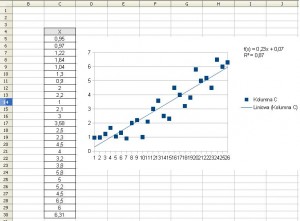 Aby obliczyć prognozy wystarczy dodać kolumnę określającą czas t z lewej strony i sprawdzić jaką przyjmuje kolejną wartość, na podstawie tej wartości obliczamy prognozę:
Aby obliczyć prognozy wystarczy dodać kolumnę określającą czas t z lewej strony i sprawdzić jaką przyjmuje kolejną wartość, na podstawie tej wartości obliczamy prognozę:
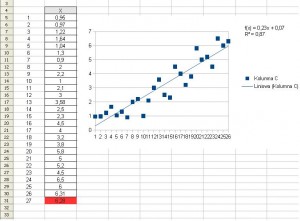 Arkusz kalkulacyjny można pobrać tutaj: wykres rozrzutu szeregu czasowego
Arkusz kalkulacyjny można pobrać tutaj: wykres rozrzutu szeregu czasowego
Prognozowanie na podstawie autoregresji
Aby obliczyć prognozę na podstawie rozrzutu wykresu autoregresji będziemy musieli do arkusza wprowadzić naszą zmienną wraz z tą samą zmienną przesuniętą w czasie.
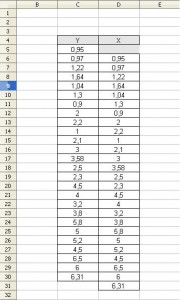 Następnie dodajemy wykres rozrzutu tylko dla danych ze sobą powiązanych:
Następnie dodajemy wykres rozrzutu tylko dla danych ze sobą powiązanych:
 Następnie wstawiamy krzywą regresji, następnie po otrzymaniu wzoru dodajemy kolejno prognozy:
Następnie wstawiamy krzywą regresji, następnie po otrzymaniu wzoru dodajemy kolejno prognozy:
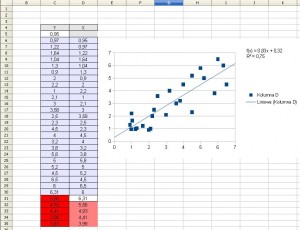 Arkusz kalkulacyjny można pobrać tutaj: wykres rozrzutu autoregresja
Arkusz kalkulacyjny można pobrać tutaj: wykres rozrzutu autoregresja
Wszystkie te operacje zrobicie bez problemu w programie : Wykres rozrzutu wersja 1.2
Więcej informacji o programie znajdziecie na stronie :
https://visualmonsters.cba.pl/index.php/pomoc-i-obsluga-programu-do-generowania-wykresow-rozrzutu