Omówimy sobie dzisiaj funkcje korelacji, autokorelacji (ACF) i autokorelacji cząstkowej (PACF). Przedstawię proste przykłady, które pomogą wam ją zrozumieć i wykorzystać do prognozowania.
Program do obliczanie ACF, PACF i korelacji znajdziecie tutaj: Funkcja ACF PACF i korelacja wersja 1.2 b
Korelacja
Zaczniemy od zwykłej korelacji. Korelacja przyjmuje wartość od -1 do 1. Brak korelacji następuje, wtedy gdy wartość korelacji wynosi 0. Dane mogą być skorelowane dodatnio albo ujemnie. Wzór na korelację wygląda następująco:
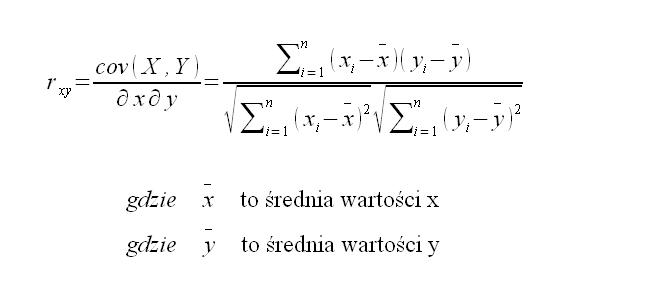 Najpierw zrobimy sobie to w Excelu, a następnie pokażę jak zrobić to w moim autorskim programie.
Najpierw zrobimy sobie to w Excelu, a następnie pokażę jak zrobić to w moim autorskim programie.
 Dokument Excel z obliczeniami dostępny tutaj: Korelacja
Dokument Excel z obliczeniami dostępny tutaj: Korelacja
Aby obliczyć taką zależność w programie do korelacji w prawym górnym rogu zaznaczamy kwadracik „Korelacja”
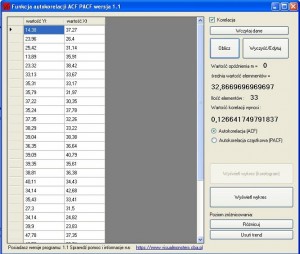
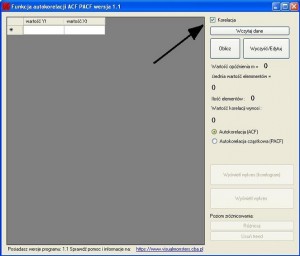 To umożliwi wprowadzenie więcej niż jednego szeregu. Dane można pobrać tutaj (dane_1,dane_2) takie jak w excelu. Wybieramy „Wczytaj dane” i eksportujemy dane do naszego programu. Po Eksporcie przyciskamy przycisk „Oblicz” i program sam obliczy korelacje.
To umożliwi wprowadzenie więcej niż jednego szeregu. Dane można pobrać tutaj (dane_1,dane_2) takie jak w excelu. Wybieramy „Wczytaj dane” i eksportujemy dane do naszego programu. Po Eksporcie przyciskamy przycisk „Oblicz” i program sam obliczy korelacje.
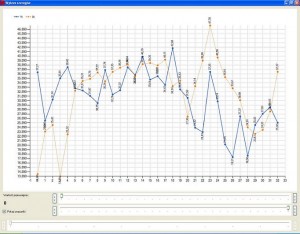
 Oba wykresy nałożone na siebie można obejrzeć po wciśnięciu przycisku „Wyświetl wykres”
Oba wykresy nałożone na siebie można obejrzeć po wciśnięciu przycisku „Wyświetl wykres”
 Wartość korelacji rzędu 0,13 oznacza bardzo niską korelację. Gdy szereg jest słabo skorelowany, a zdaje się nam, że dane są w jakiś sposób zależne, warto spróbować zróżnicować szereg i aby sprawdzić, czy może ich przyrosty są skorelowane. Przyciskamy przycisk „Różnicuj” w głównym oknie programu, dane powinny ulec zmianie według wzoru:
Wartość korelacji rzędu 0,13 oznacza bardzo niską korelację. Gdy szereg jest słabo skorelowany, a zdaje się nam, że dane są w jakiś sposób zależne, warto spróbować zróżnicować szereg i aby sprawdzić, czy może ich przyrosty są skorelowane. Przyciskamy przycisk „Różnicuj” w głównym oknie programu, dane powinny ulec zmianie według wzoru:
wygląda to tak:
 Wykres szeregów po różnicowaniu:
Wykres szeregów po różnicowaniu:
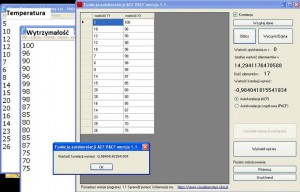
 Wartość korelacji jest równa 0,2568, co świadczy o większej korelacji przyrostów szeregu. Korelację wykorzystujemy zazwyczaj, aby sprawdzić zależności takie jak na przykład wpływ zarobków Polaków na sprzedaż alkoholu w Polsce 😛 albo wpływ zamiany temperatury na wytrzymałość na przykład plastiku. Powiedzmy, że stworzymy dwa szeregi, jeden to będzie temperatura w Celsjuszach, a drugi będzie wytrzymałością takiego plastiku 😛 plastik ma wytrzymałość 100, jeśli temperatura będzie niska, jego wytrzymałość maleje wraz ze wzrostem temperatury. Jaki będzie wynik korelacji:
Wartość korelacji jest równa 0,2568, co świadczy o większej korelacji przyrostów szeregu. Korelację wykorzystujemy zazwyczaj, aby sprawdzić zależności takie jak na przykład wpływ zarobków Polaków na sprzedaż alkoholu w Polsce 😛 albo wpływ zamiany temperatury na wytrzymałość na przykład plastiku. Powiedzmy, że stworzymy dwa szeregi, jeden to będzie temperatura w Celsjuszach, a drugi będzie wytrzymałością takiego plastiku 😛 plastik ma wytrzymałość 100, jeśli temperatura będzie niska, jego wytrzymałość maleje wraz ze wzrostem temperatury. Jaki będzie wynik korelacji:
Wnioski same, się nasuwają, wysoka korelacja ujemna -0,98 wskazuje, że dwa szeregi są bardzo mocno skorelowana, kiedy jeden szereg rośnie, drugi maleje. (dane do pobrania dla tego eksperymentu: temp,wtyrz_plastiku)
Autokorelacja ACF
Autokorelacja jest to proces zbliżony do korelacji, z tą różnicą, że podczas korelacji szereg korelowany jest z samym sobą. Wzór na autokorelacje wygląda tak:
Stwórzmy nawy plik excel i dodajmy sobie szereg:
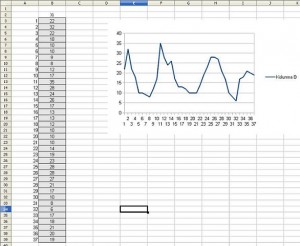 Aby wyznaczyć wartości korelacji rzędu 1 musimy dodać sobie szereg przesunięty o 1. Sposób obliczenia prezentuje w pliku
Aby wyznaczyć wartości korelacji rzędu 1 musimy dodać sobie szereg przesunięty o 1. Sposób obliczenia prezentuje w pliku
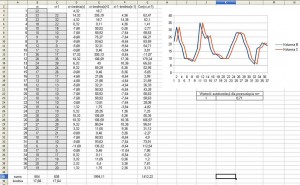 excel:Autokorelacja cz1
excel:Autokorelacja cz1
Nasz szereg na poziomie m=1 skorelowany z samym sobą na poziomie 0,71. Dodamy kolejne przesunięcie:
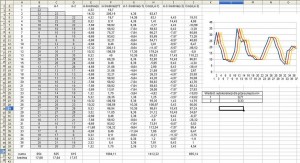 plik excel: Autokorelacja cz2
plik excel: Autokorelacja cz2
Dodamy sobie jeszcze jedno przesunięcie:
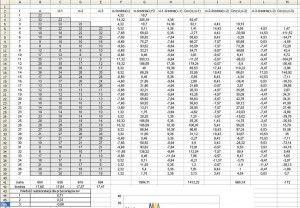 plik excel: Autokorelacja cz3
plik excel: Autokorelacja cz3
Powtórzenie takich obliczeń 10 razy wygeneruje nam wystarczającą ilość współczynników autokorelacji aby utworzyć z nich sensowny korelogram:
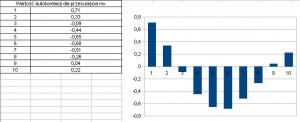 plik excel: Autokorelacja cz4
plik excel: Autokorelacja cz4
Każdy z was kto miał do czynienia z korelogramami może zauważyć, że naszemu coś brakuje. Tak brakuje poziomów ufności. Są dwa poziomy ufności. Jeśli słupki korelogramu w większości znajdują się poniżej poziomu ufności mamy prawo sądzić, że nasz szereg jest czysto losowy. Pierwszy jest na stałym poziomie:
 Drugi jest trochę bardziej skomplikowany. Różni się on tym od pierwszej, że wraz ze wzrostem czasu t jego wartość rośnie lub maleje dla korelacji ujemnych. Ma to sens, ponieważ jeśli idziemy w czasie do przodu i mamy coraz mniej danych, dane tracą na aktualności. Nazywany jest Dużym 95% poziomem ufności, opisuje się ją wzorem:
Drugi jest trochę bardziej skomplikowany. Różni się on tym od pierwszej, że wraz ze wzrostem czasu t jego wartość rośnie lub maleje dla korelacji ujemnych. Ma to sens, ponieważ jeśli idziemy w czasie do przodu i mamy coraz mniej danych, dane tracą na aktualności. Nazywany jest Dużym 95% poziomem ufności, opisuje się ją wzorem:
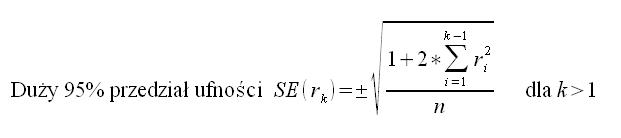 W excelu ich obliczanie wygląda następująco:
W excelu ich obliczanie wygląda następująco:
plik excel: Autokorelacja + przedzialy ufnosci
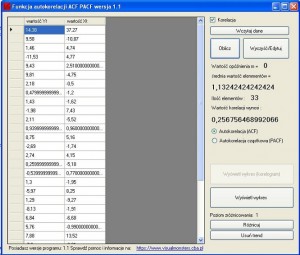
 Liczenie autokorelacji w Excelu to bardzo żmudny proces, warto sięgnąć tutaj po program, który zrobi to za nas i przedstawi dane w zrozumiały sposób. Program, który tutaj zaprezentuje, ma takie możliwości. Przedstawię tutaj analizę tego samego szeregu. Po załadowaniu szeregu do programu (dane_1_autokorelacja) klikamy przycisk „Oblicz”
Liczenie autokorelacji w Excelu to bardzo żmudny proces, warto sięgnąć tutaj po program, który zrobi to za nas i przedstawi dane w zrozumiały sposób. Program, który tutaj zaprezentuje, ma takie możliwości. Przedstawię tutaj analizę tego samego szeregu. Po załadowaniu szeregu do programu (dane_1_autokorelacja) klikamy przycisk „Oblicz”
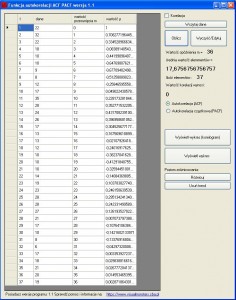
 Po kliknięciu program zapyta jaką wartość autokorelacji chcemy obliczyć, pozostawienie pustego pola spowoduje obliczenie maksymalnej ilości korelacji. Tak właśnie zrobimy. Obliczenia wyglądają tak:
Po kliknięciu program zapyta jaką wartość autokorelacji chcemy obliczyć, pozostawienie pustego pola spowoduje obliczenie maksymalnej ilości korelacji. Tak właśnie zrobimy. Obliczenia wyglądają tak:
 Teraz możemy otworzyć korelogram:
Teraz możemy otworzyć korelogram:
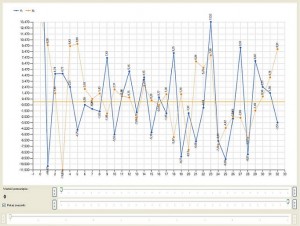
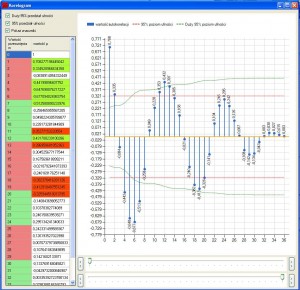 Nad poziomem ufności mamy wiele zmiennych, ale największą ujemną korelację otrzymujemy dla przesunięcia o wartość 6, a największą dodatnią korelację dla przesunięcia 12, im danych jest mniej do korelowania, tym nasze słupki są mniejsze. Aby bardziej zobrazować sobie sytuacje, jaka ma miejsce w autokorelacji, można na głównej formie otworzyć „Wyświetl wykres” i przesunąć drugi najpierw o wartość 6, a następnie o 12:
Nad poziomem ufności mamy wiele zmiennych, ale największą ujemną korelację otrzymujemy dla przesunięcia o wartość 6, a największą dodatnią korelację dla przesunięcia 12, im danych jest mniej do korelowania, tym nasze słupki są mniejsze. Aby bardziej zobrazować sobie sytuacje, jaka ma miejsce w autokorelacji, można na głównej formie otworzyć „Wyświetl wykres” i przesunąć drugi najpierw o wartość 6, a następnie o 12:
Przesunięcie o wartość 6:
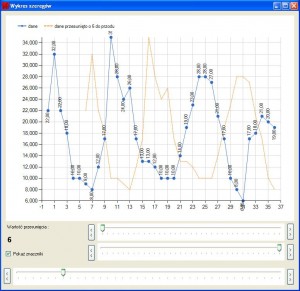 Widać, że tam gdzie wartości szeregu przesuwanego rosną wartości szeregu niebieskiego maleją. Sprawdźmy 12:
Widać, że tam gdzie wartości szeregu przesuwanego rosną wartości szeregu niebieskiego maleją. Sprawdźmy 12:
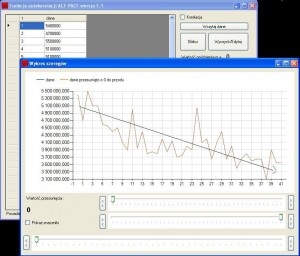
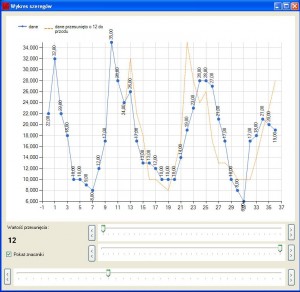 Wykresy nakładają się. Jaki może płynąć z tego wniosek, otóż nasz szereg posiada sezon powtarzający się co 12 okresów 6 spadków następnie 6 wzrostów i tak dalej. Sprawdzamy, na jakim etapie znajduje się wykres i podejmujemy decyzję czy szereg będzie kontynuował wzrosty czy może spadki. Dodatkową funkcję jaką posiada program, jest usuwanie trendu. Spójrzmy na wykres danych poniżej, można zaobserwować wyraźny trend spadkowy.
Wykresy nakładają się. Jaki może płynąć z tego wniosek, otóż nasz szereg posiada sezon powtarzający się co 12 okresów 6 spadków następnie 6 wzrostów i tak dalej. Sprawdzamy, na jakim etapie znajduje się wykres i podejmujemy decyzję czy szereg będzie kontynuował wzrosty czy może spadki. Dodatkową funkcję jaką posiada program, jest usuwanie trendu. Spójrzmy na wykres danych poniżej, można zaobserwować wyraźny trend spadkowy.
 Wykres autokorelacji dla takiego szeregu wygląda następująco:
Wykres autokorelacji dla takiego szeregu wygląda następująco:
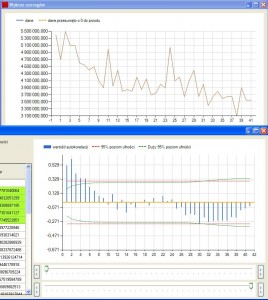 Trend usuwa się w głównym oknie programu za pomocą przycisku „Usuń trend”. Po jego naciśnięciu nad przyciskiem „Wyświetl korelogram” pokażą się dwie dodatkowe wartości. Wzór na trend będzie wyglądał następująco:
Trend usuwa się w głównym oknie programu za pomocą przycisku „Usuń trend”. Po jego naciśnięciu nad przyciskiem „Wyświetl korelogram” pokażą się dwie dodatkowe wartości. Wzór na trend będzie wyglądał następująco:
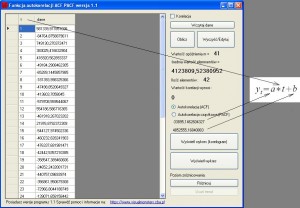 Po ponownym obliczeniu nasz korelogram będzie wyglądał inaczej, czasem bardziej czytelnie.
Po ponownym obliczeniu nasz korelogram będzie wyglądał inaczej, czasem bardziej czytelnie.
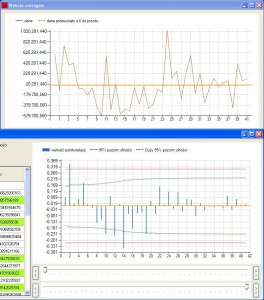 Dzięki takiej operacji można często wyodrębnić dane niezauważalne na pierwszy rzut oka. Oczywiście takie szeregi można również z powodzeniem różnicować. Autokorelacja często używana jest do podejmowania decyzji podczas tworzenia modeli ARMA, ARIMA.
Dzięki takiej operacji można często wyodrębnić dane niezauważalne na pierwszy rzut oka. Oczywiście takie szeregi można również z powodzeniem różnicować. Autokorelacja często używana jest do podejmowania decyzji podczas tworzenia modeli ARMA, ARIMA.
Autokorelacja cząstkowa PACF
Auto korelacja cząstkowa to bardziej skomplikowany proces. Ciężko cokolwiek konkretnego na ten temat znaleźć w internecie, a już na pewno wzór na obliczanie tej zależności. Do obliczenia PACF potrzebne będą wartości ACF, za ich pomocą oblicza się współczynniki dla wzoru. Auto korelacja cząstkowa mierzy zależność liniową jednej zmiennej po usunięciu innej zmiennej, która ma wpływ na obie zmienne. Na przykład autokorelacja cząstkowa dla yt-2 po usunięciu wpływu yt-1 zarówno dla yt jak i yt-2.
Każdą autokorelacje cząstkową można przedstawić w postaci szeregu regresji:
 Najlepszą metodą do oszacowania estymatorów tworzących szereg regresji jest układ równań normalnych. Tworzymy sobie macierz złożoną z parametrów naszego szeregu:
Najlepszą metodą do oszacowania estymatorów tworzących szereg regresji jest układ równań normalnych. Tworzymy sobie macierz złożoną z parametrów naszego szeregu:
 Następnie z własności macierzy wiemy, że aby obliczyć nasze współczynniki, czyli wartości autokorelacji cząstkowej musimy pomnożyć prawą stronę przez macierz odwrotną lewej strony:
Następnie z własności macierzy wiemy, że aby obliczyć nasze współczynniki, czyli wartości autokorelacji cząstkowej musimy pomnożyć prawą stronę przez macierz odwrotną lewej strony:
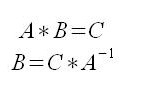 Aby pokazać wam obliczenia w excelu skorzystamy ze starego pliku w którym mamy już obliczone wartości autokorelacji i gotowy wykres
Aby pokazać wam obliczenia w excelu skorzystamy ze starego pliku w którym mamy już obliczone wartości autokorelacji i gotowy wykres
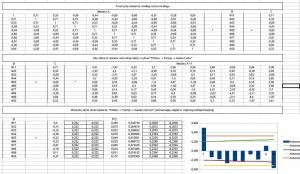 Plik excel do pobrania tutaj: Autokorelacja cząstkowa + przedzialy ufnosci
Plik excel do pobrania tutaj: Autokorelacja cząstkowa + przedzialy ufnosci
Nie ą to obliczenia aż tak skomplikowane, ale gdy mamy do czynienia z dużo większą ilością danych albo dane te są bardzo drobnicowe, wtedy możemy chcieć obliczyć, autokorelację cząstkową wyższego rzędu co może przysporzyć trochę kłopotów. Odpalamy program do obliczeń, wczytujemy dane i po prawej stronie zmieniamy z „Autokorelacja (ACF)” na „Autokorelacja cząstkowa (PACF)”.
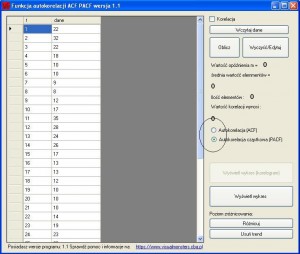 Klikamy oblicz i wpisujemy przedział 10, co automatycznie obliczy nam autokorelację cząstkową dla takiego rzędu. Jej korelogram wygląda tak:
Klikamy oblicz i wpisujemy przedział 10, co automatycznie obliczy nam autokorelację cząstkową dla takiego rzędu. Jej korelogram wygląda tak:
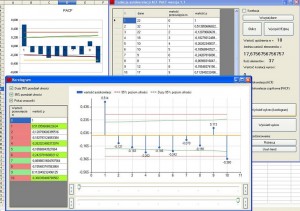 Podczas obliczania można nie wpisywać wartości opóźnienia, co da nam wgląd na wszystkie możliwe wartości autokorelacji cząstkowej:
Podczas obliczania można nie wpisywać wartości opóźnienia, co da nam wgląd na wszystkie możliwe wartości autokorelacji cząstkowej:
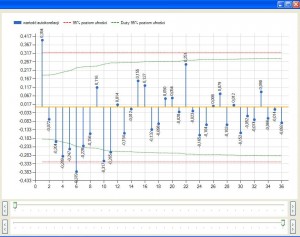 Tak jak poprzednio można usuwać trend i różnicować nasz szereg aż do uzyskania wyraźnego interesującego nas sygnału. Autokorelacje cząstkowa często używana jest do podejmowania decyzji podczas tworzenia modeli ARMA, ARIMA.
Tak jak poprzednio można usuwać trend i różnicować nasz szereg aż do uzyskania wyraźnego interesującego nas sygnału. Autokorelacje cząstkowa często używana jest do podejmowania decyzji podczas tworzenia modeli ARMA, ARIMA.
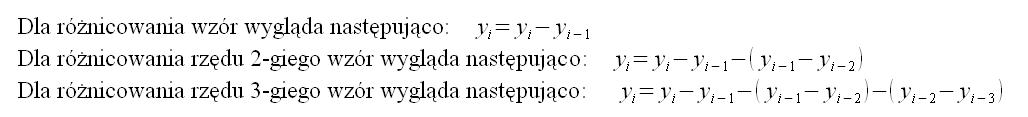
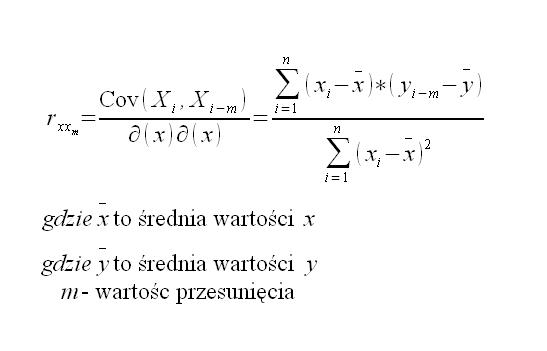


1 komentarz
Cześć,
Bardzo dobry artykuł, dziękuję za podzielenie się!
Mam tylko jedną wątpliwość, jeżeli chodzi o obliczenia – czy nie powinniśmy brać równej liczby obserwacji dla szeregów Xt i Xt-n?
Przykład: Jeżeli mamy, przypuśćmy, 5 rząd opóźnień, to dla szeregu Xt-5 będziemy mieć 5 obserwacji mniej niż Xt. Zatem do wzoru na autokorelację jesteśmy w stanie obliczyć o 5 składników licznika mniej niż dla mianownika. Czyż nie powinniśmy zrezygnować z sumowania pierwszych 5 iloczynów?