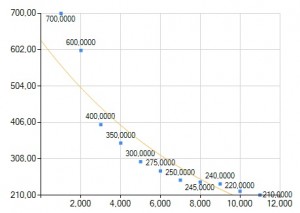
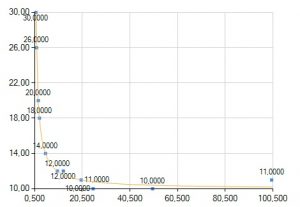
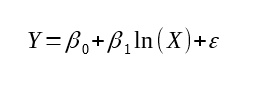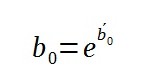Trend to pewien rodzaj prostej funkcji, która determinuje nasze elementy szeregu. Można za jego pomocą w prosty sposób prognozować, chociaż taka prognoza w wypadku szeregów czasowych jest mało efektywna, ale za ich pomocą możemy stwierdzić jaki ogólny przebieg może mieć szereg w przyszłości. Tren dzielimy na te liniowe, nieliniowe sprowadzane do liniowych i te niesprowadzane do liniowych.
Większość średnich można w łatwy sposób obliczać za pomocą minimum:
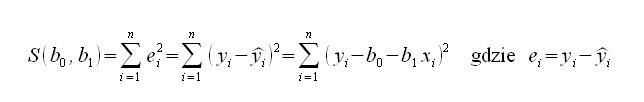
Artykuł zawiera opis modeli trendów:
- Liniowych
- Logarytmicznych
- Potęgowych
- Wykładniczych
- Hiperbolicznych
Do artykułu będę systematycznie dodawała modele trendów. Wszystkie wykresy zawarte w artykule zostały wykonane przy użyciu programu:
Program do generowania wykresów rozrzutu
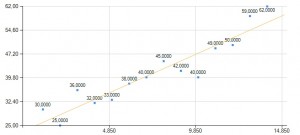
Model trendu liniowego
. Wzór modelu wygląda następująco:
 gdzie:
gdzie:
Y – Zmienna objaśniana.
X – zmienna objaśniająca.
β1 i β0 – parametry strukturalne.
ε – Składnik losowy.
Aby wyznaczyć przybliżone wartości parametrów β1≈b1 i β0≈b0 stosuje się metodę najmniejszych kwadratów. Najpierw musimy wyznaczyć minimum funkcji
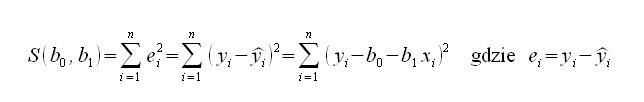
Następnie po przekształceniu wzory wyliczamy pochodne dla
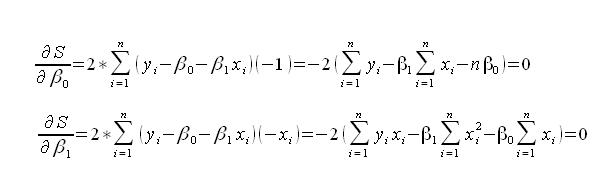 Po przekształceniu ostatecznie uzyskujemy wzór na obliczenie przybliżonych parametrów b1 i b0.
Po przekształceniu ostatecznie uzyskujemy wzór na obliczenie przybliżonych parametrów b1 i b0.
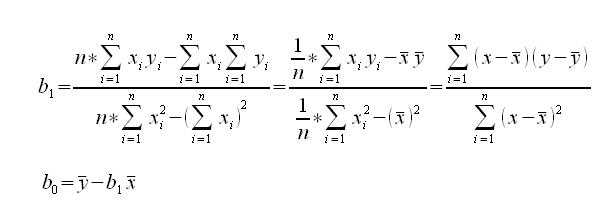
Przykład obliczeń w pliku Excel: przykład_trend_liniowy.odt , przykład_trend_liniowy.xls
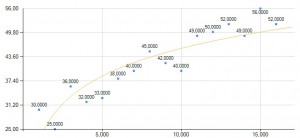
Model trendu logarytmicznego
Wzór modelu wygląda następująco:
Y – Zmienna objaśniana.
X – zmienna objaśniająca.
β1 i β0 – parametry strukturalne.
ε – Składnik losowy.
Aby wyznaczyć przybliżone wartości parametrów β1≈b1 i β0≈b0 stosuje się metodę najmniejszych kwadratów. Najpierw musimy wyznaczyć minimum funkcji
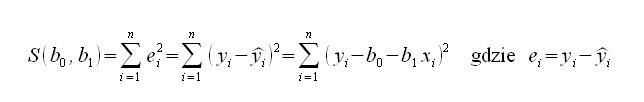
Cały trik polega na tym, że stosujemy podstawienie
![]()
Co sprowadza nasz model do klasycznej postaci liniowej:
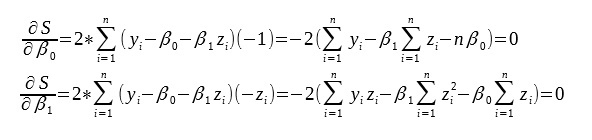
Po przekształceniu ostatecznie uzyskujemy wzór na obliczenie przybliżonych parametrów b1 i b0.
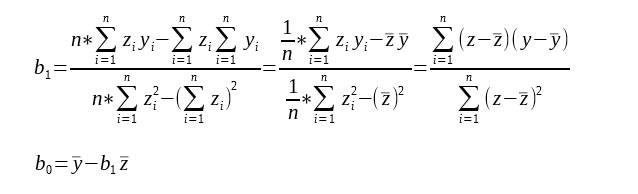
Przykład obliczeń w Excelu: przykład_trend_logarytmiczny.ods , przykład_trend_logarytmiczny.xls
Model trendu potęgowego
Wzór modelu wygląda następująco::
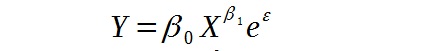
gdzie:
Y – Zmienna objaśniana.
X – zmienna objaśniająca.
β1 i β0 – parametry strukturalne.
ε – Składnik losowy.
e – liczba Napiera (Napera)
Aby sprowadzić do klasycznej postaci liniowej należy przeprowadzić operacje:
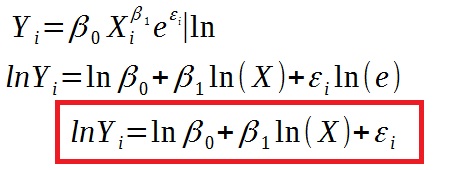
Teraz wystarczy tylko podstawić zmienne:
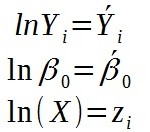
Aby wyznaczyć przybliżone wartości parametrów β1≈b1 i β0≈b0 stosuje się metodę najmniejszych kwadratów.
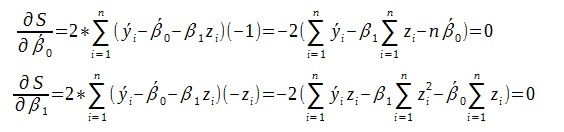
Po przekształceniu ostatecznie uzyskujemy wzór na obliczenie przybliżonych parametrów b1 i b0.
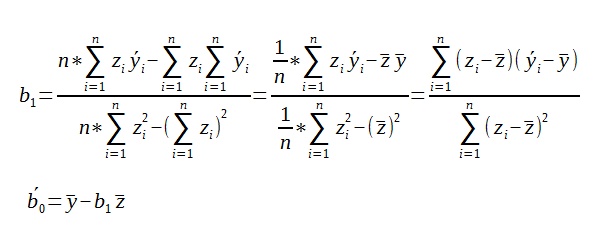
Ostatecznie b0 obliczymy:
Przykład obliczeń w Excelu: Model-potegowy-zależny-przyklad.ods, Model-potegowy-zależny-przyklad.xls
Dodatkowo: przykład_trend_potęgowy.ods, przykład_trend_potęgowy.xls
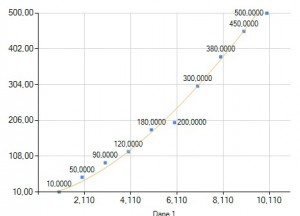
Model trendu wykładniczego
Wzór modelu wygląda następująco:
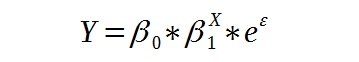
gdzie:
Y – Zmienna objaśniana.
X – zmienna objaśniająca.
β1 i β0 – parametry strukturalne.
ε – Składnik losowy.
e – liczba Napiera (Napera)
Tak jak poprzedni, poprzez logarytmowanie sprowadzimy sobie go do postaci liniowej:
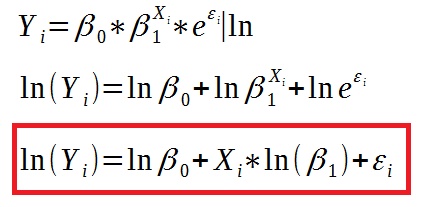
Należy teraz podstawić pod logarytmy niewiadome:
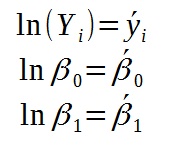
Aby wyznaczyć przybliżone wartości parametrów β1≈b1 i β0≈b0 stosuje się metodę najmniejszych kwadratów.
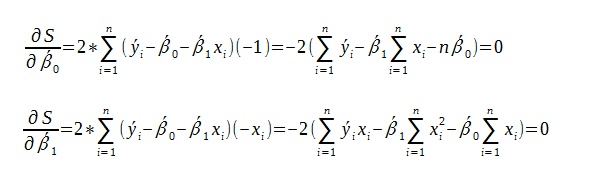
Po przekształceniu ostatecznie uzyskujemy wzór na obliczenie przybliżonych parametrów b1 i b0.
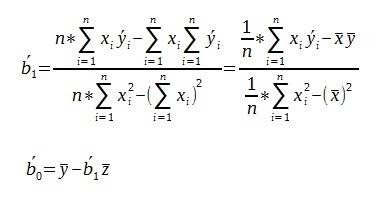
Ostatecznie prognozę wygasłą obliczamy ze wzoru:
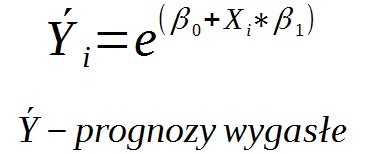
Przykład obliczeń w Excelu: przykład_trend_wykładniczy.ods, przykład_trend_wykładniczy.xls
Model trendu hiperbolicznego
Wzór modelu wygląda następująco: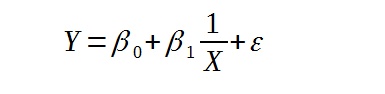
Y – Zmienna objaśniana.
X – zmienna objaśniająca.
β1 i β0 – parametry strukturalne.
ε – Składnik losowy.
Aby obliczyć tego typu trend, wystarczy, że dokonamy podstawienia:
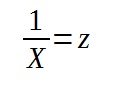
Aby wyznaczyć przybliżone wartości parametrów β1≈b1 i β0≈b0 stosuje się metodę najmniejszych kwadratów.
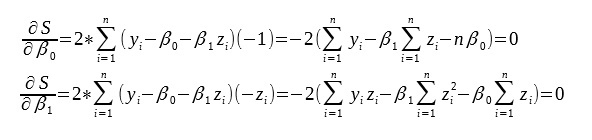
Po przekształceniu ostatecznie uzyskujemy wzór na obliczenie przybliżonych parametrów b1 i b0.
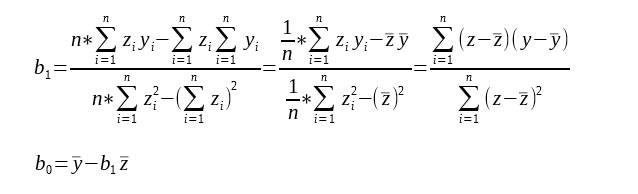
Przykład obliczeń w Excelu:przykład_trend_hiperboliczny.ods, przykład_trend_hiperboliczny.xls